The attraction of the pyramids: virtual realization of Hutton's suggestion to improve Maskelyne's 1774 Earth density estimate

Charles Hutton suggested in 1821 that the pyramids of Egypt be used to site an experiment to measure the deflection of the vertical by a large mass. The suggestion arose as he had estimated the attraction of a Scottish mountain as part of Nevil Maskelyne's (1774) “Schiehallion Experiment”, a demonstration of Isaac Newton's law of gravitational attraction and the earliest reasonable quantitative estimate of Earth's mean density. I present a virtual realization of an experiment at the Giza pyramids to investigate how Hutton's concept might have emerged had it been undertaken as he suggested. The attraction of the Great Pyramid would have led to inward north–south deflections of the vertical totalling 1.8 arcsec (0.0005^∘), and east–west deflections totalling 2.0 arcsec (0.0006^∘), which although small, would have been within the contemporaneous detectable range, and potentially given, as Hutton wished, a more accurate Earth density measurement than he reported from the Schiehallion experiment.

1 Introduction

Following his analysis as part of Astronomer Royal Nevil Maskelyne's experiment to measure Earth's mean density on the Scottish mountain Schiehallion in 1774, Charles Hutton suggested that another plumb-line experiment at a geometrically simpler large mass would be preferable to address some of the challenges he had encountered (Maskelyne, 1775a; Hutton, 1821). His suggestion was that a similar experiment be conducted at the pyramids in Giza, Egypt (Fig. 1). A digital realization of such an experiment at the Giza pyramids is presented here to investigate what could have resulted from Hutton's concept.

On a uniform spherical Earth, plumb-lines would hang so as to point towards the Earth's centre, its centre of mass. However, a hanging plumb-line is deflected if a nearby mass attracts the plumb-bob (or plummet) (Fig. 2a). The deflection is very small, as outweighing the advantage of its proximity, the mass is small relative to the mass of the Earth.

2 Background

In the late 17th century, Isaac Newton proposed two experimental methods by which the mass of the Earth could be measured. One of his proposals was to measure the force of attraction between two known masses in the laboratory, and the other was to measure the deflection of a weight on a plumb-line towards a “hill”. Newton took as an example a hypothetical hemispherical mountain with a height of 3 miles and a basal diameter of 6 miles. He calculated that, if the mountain had the same density as the Earth, the mountain would “by its attraction, draw the plumb-line [less than] 2 min out of the perpendicular” (Newton, 1731), recognizing that the measurement of such a deflection presented a challenge for the experimentalists of his day.

Figure 1 Topography of the study area (Becker et al., 2009). Black triangle: the location of the Giza pyramids, towards the north of the River Nile in Egypt. Red line: location of the profile in Fig. 2c. The presence of the Mediterranean Sea contributes to a southward deflection of the vertical at Giza, to the south, but the difference in the effect between nearby stations is negligible.

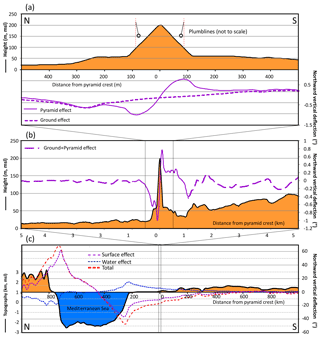
Figure 2 North–south profile of topography and computed northward deflection of the vertical through the Great Pyramid. Location shown in Fig. 1. (a) 1 km section. The summed inward deflection between the northern and southern flanks of the pyramid is 1.8 arcsec. The component of the deflection of the vertical caused by the surrounding ground topography is indicated with the dashed line. The pyramid continues to cause a difference in deflection of the vertical greater than about 0.1 arcsec for a distance of about 300 m from its peak. (b) 10 km section. More regionally, the deflection of the vertical in a north–south direction is greatest on the pyramid's faces, but the topography also causes variations up to about 0.3 arcsec. (c) 2000 km section. Regional effect of the surface and Mediterranean Sea. Here densities of 1050 and 2500 km m⁻³ have been used for water and topography respectively. The strongest deflections of the vertical (red trough and peak at 700 and 250 km N on the profile) are associated with the relatively sharp changes in bathymetry on the margins of the sea. A deflection of the vertical of about 11 arcsec south is calculated at Giza, largely due to the lateral topographic and density contrast between the water body of the Mediterranean Sea and the topography of southern Egypt, though the difference between the stations on the pyramid flanks is negligible.

The first attempt to carry out the plumb-line deflection experiment was that of Pierre Bouguer, who, encouraged by the scale of the Andean mountains, undertook such an experiment in 1738 as one of his contributions to the Paris Academy's meridian arc expedition (Bouguer, 1749). Before attempting the experiment, Bouguer estimated that the Andean mountain Chimborazo would give a plumb-line deflection of 1^′43${}^{\prime \prime }$ (0.03^∘). Stellar observations from a position on the snowline on the southern flank of Chimborazo, and from a lower second station to the west of the mountain, showed a much smaller observed deflection of the vertical than he predicted: just 7.5 arcsec (0.002^∘). Bouguer concluded his report with the hope that a mountain of sufficient size in France or England could be identified for a plumb-line experiment, so that measurements could be made both in more benign conditions and with an improved experimental layout utilizing stations to the north and south of a mountain, doubling the deflection effect being measured. Although recent modelling has suggested his measured deflection was as would be expected from the topography (Smallwood, 2010), the apparent discrepancy encouraged further plumb-line experiments to be undertaken.

Such an attempt was proposed in 1772 by Revd. Nevil Maskelyne, the British Astronomer Royal. In scoping this proposed experiment, Maskelyne returned to Newton's hemispherical mountain and “by a very easy calculation [stated] that such a mountain would attract the plumb-line 1^′18${}^{\prime \prime }$ from the perpendicular” (Maskelyne, 1775a). However, isolated real mountains on such a scale are unusual, and the deflection of the vertical caused by real mountains is normally much smaller than that in Newton's example. Furthermore, as Maskelyne appreciated, the shallow density of crustal rocks is often less than half the Earth's mean density, and that makes any plumb-line deflection an even smaller quantity. Maskelyne detected the deflection of plumb-lines towards Schiehallion by taking astronomical observations at two temporary observatory stations on the northern and southern flanks of the mountain. The difference between astronomically determined latitude separation of the two observatories and their surveyed locations yielded the gravitational attraction of the mountain relative to that of the earth. Maskelyne (1775b) offered the preliminary finding that, “… the mean density of the earth is at least double of that at the surface …”, and that “The whole quantity of matter in the earth … will be about four or five times as great as if it were all composed of water”.

The precision of Maskelyne's zenith sector was sufficient to yield a measurement of the mean sum of the two plumb-line deflections towards Schiehallion which he quoted as 11.66${}^{\prime \prime }$, rounded down to 11.6${}^{\prime \prime }$ (0.00322^∘) in his final statement of results. This sum of deflections, though small, was treated with confidence and taken forward to give an Earth mean density estimate. This calculation of Earth's density relied on the measurement of the mountain's mass, which required a detailed topographic survey, conducted between 1774 and 1776, and extensive geometric modelling. Charles Hutton carried out the conversion of the survey measurements into the expected plumb-line deflections (Hutton, 1778). After analysis of the topographic survey, Hutton was able to improve on the precision of Maskelyne's preliminary estimate and report a mean Earth density of 4500 kg m⁻³. In doing so, Hutton noted that the reduction of the topographic survey data was labour intensive, and though it had been selected for its favourable geometry, the mountain's irregularity led to a somewhat laborious and maybe inaccurate calculation. Weather conditions had been challenging, and the “inconveniences” of the Scottish mountainside contributed towards Maskelyne's Royal Society Copley Medal award in 1775 (Higgitt, 2014).

Hutton subsequently reviewed the experimental analysis, giving a final average Earth density estimate of 4950 kg m⁻³ (Hutton, 1821), commendably accurate, but still some way short of the currently accepted average density value of 5515 kg m⁻³ (Lowrie, 1997).

Hutton laid down a challenge to his successors: “let any person … look over and repeat the calculations … and try if he can find any inaccuracy in them” (Hutton, 1821). Also, recognizing the challenges of the variable topography of Schiehallion, Hutton suggested the Egyptian pyramids as offering considerable advantages for a plumb-line experiment: “I cannot conclude this paper of enquiry, without expressing a hearty wish for the repetition of the large or mountain experiment, in some other favourable situation, and with improved means, if possible. For this purpose, I shall venture just to mention an idea which has sometimes occurred to my mind, namely, that one of the large pyramids in Egypt might profitably be employed, instead of a mountain, for this experiment. Such a body offers several advantages for the purpose. In the first place, the mass is sufficiently large, standing on a base of about the whole space of Lincoln's Inn Fields, and of a height almost double that of St. Paul's steeple; then the station for the plummet, or zenith sector, could be taken much nearer the centre of mass, than on a mountain, which would give a larger quantity of deviation of the plummet; then the regular figure and the known composition of the mass would yield great facilities in the calculation of its attraction; lastly, the deviation of the plummet might be observed on all the four sides. Should such a project take place, it will be best to take the stations at about one fourth of its altitude above the base, that being the place where the deviation of the plummet would be the greatest. Finally, so favourable for such an experiment do those circumstances appear, and so anxious are my wishes for its completion and success, that, were it not for my great age and little health, I should be glad to make one in any party to undertake such an expedition.” (Hutton, 1821). In his preference for a geometrically simpler gravitational attractor, Hutton followed Maskelyne's reflection on the Schiehallion experiment (Maskelyne, 1775b): “Some may doubt whether the density of matter near the surface of the earth may not be subject to considerable variation”, and “… it becomes a matter of great importance to chuse [sic] those places for measuring degrees, where the irregular attractions of the elevated parts may be small”.

Maskelyne had confidence in his ability to measure small deflections; in his proposal for the Schiehallion experiment, at a time the experimental site had not been determined, he considered that deflections of 6 or 9 arcsec (at Whernside in Yorkshire) or 4 arcsec (at Threlkeld in the Lake District) would be within his range of detectability: “… quantities are not too small to be measured and demonstrated by an accurate zenith sector …” (Maskelyne, 1775a). He also reported his Schiehallion findings in arcsec to two decimal places, indicating considerable confidence in their resolution, and had sufficient confidence in his 11.6 arcsec measurement for the topographic mountain survey to proceed over several years. Reeves (2009) argues that a significant motivation for Maskelyne to spend a lengthy period of time away from the Royal Observatory in Greenwich in 1774 was to demonstrate the precision of his zenith sector instrument, which was not widely extant at this time, but in which he had considerable confidence. The zenith sector pointed vertically upwards, direction referenced to the plumb-line. A pivot-mounted telescope allowed Maskelyne to precisely measure the angle between a number of stars and the highest point in the sky.

Contemporaneous experimental precision can also be estimated from Maskelyne's reported apparent latitudinal difference between the two Schiehallion observatories of 54.56±1.28 arcsec (1 SD, n=20) against a geometrically surveyed latitudinal separation of 43.25±0.2 arcsec. These measurements lead to a difference attributable to the mountain's attraction of 11.3±1.3 arcsec (Smallwood, 2007). To determine this apparent latitudinal separation at Schiehallion, Maskelyne's averaging of multiple astronomical measurements was deliberate, to improve accuracy and remove any collimation errors (Maskelyne, 1775b; Reeves, 2009).

3 The Giza Plateau: regional gravity effects

The pyramids at Giza, in Cairo, Egypt, are the only largely remaining of the seven wonders of the ancient world. The oldest and largest, the “Great Pyramid”, is thought to have been built as a tomb for the Fourth Dynasty Egyptian pharaoh Khufu, with an astronomical base alignment around 2480–2560 BC (e.g. Spence, 2000). Consisting probably of over 2 million stone blocks, it is thought that the pyramid was originally 146.5 m tall, for a long time the tallest man-made structure on Earth. With erosion and the absence of its capping pyramidion, its present height is 138.8 m. Early careful measurements of the pyramid were made in 1880–1882 (Petrie, 1883). Each side of the square base was found to be 230.4 m long. The base is extremely flat, and orientations of the sides of the square base are aligned to the four compass points. Hutton's suggestion was that gravity observation stations should be positioned on each face of the pyramid, a quarter of the way up (Hutton, 1779, 1821).

To put local contributions to the gravity anomaly at the Giza pyramids into context, the crustal structure and density effects and the effect of the regional topographic variations have been considered. None of the examined geoid models had sufficient resolution to contribute to a difference in the deflection of the vertical expected between stations as close together as Hutton suggested. The most recent local geoid model (El-Ashquer et al., 2017) includes representation of the geoid up to spherical harmonic degree/order 720, i.e. a 56 km wavelength (Hofmann-Wellenhof and Moritz, 2005). At higher resolutions, topography is the dominant contributor to vertical deflections, and this has been modelled explicitly.

Publicly available gravity data have been used to directly estimate the differential deflection of the vertical between the proposed stations at Giza (Kamel and Nakhla, 1987; NGDC, 1999). As for the geoids, a negligible difference in vertical deflection between the stations is calculated from these data, as Hutton's proposed stations, each 85 m from the pyramid's crest, were very close together relative to the gravity data points, which can only imply the same deflection of the vertical at all the stations.

The effect of regional topography has been calculated directly, as the most significant density contrast causing the deflection of the vertical is the interface between the ground and air. This was modelled using topography digitized from the Giza Plateau Mapping Project within around 1 km of the pyramids (Lehner, 1997; Fig. 2a), surrounding 90 m resolution satellite-derived topography (Shuttle Radar Topography Mission, SRTM, data; Jarvis et al., 2008; Fig. 2b) and, more regionally, 30 arcsec (ca. 900 m) resolution SRTM data (Becker et al., 2009; Figs. 1 and 2c). Densities of 1050 and 2500 kg m⁻³ have been selected to model the effects of seawater and regional topography respectively and the two components of deflection combined. For comparison, Saleh (2013) used shallow crustal densities ranging from 2100 kg m⁻³ for sediments in the Mediterranean Sea and 2350 kg m⁻³ in the Nile Cone, up to 2580 kg m⁻³ for “Messinian compact sediments”, while 2300 kg m⁻³ was used for computation of the Bouguer gravity anomaly across Egypt (Kamel and Nakhla, 1987; NGDC, 1999).

An overall southerly deflection of the vertical attributable to the topography of about 11 arcsec is calculated at Giza, largely due to the large-scale lateral topographic contrast between the water body of the Mediterranean Sea and the topography of southern Egypt (Fig. 2c). Just as for the regional geoid and gravity anomaly-derived deflection of the vertical, however, relatively closely spaced observatory stations at Giza experience very little differential effect from the topography. The model suggests that the total sum of inward deflections of the vertical caused by the topography around the pyramids would be about 10 % that from the pyramid alone, with most of that originating within a few hundred metres of the pyramid (Fig. 2a).

To summarize, the regional effects may be significant in magnitude, but they do not supply a meaningful differential between stations as close to each other as Hutton suggested on the flanks of the pyramid would have been. A similar finding applied to Bouguer's experiment in Ecuador/Peru, even though those observatories were much further apart than Hutton's pyramid suggestions (Smallwood, 2010). Hutton's instinct that the pyramid itself would give rise to the predominant part of the deflection signal was correct.

4 The Giza Plateau: local gravity modelling

The rocks comprising the Giza Plateau on which the pyramid sits are Eocene-age limestones and the majority of the Great Pyramid itself consists almost exclusively of limestone of local provenance (Klemm and Klemm, 2001). Some large granite stones are present within the pyramid, but these are volumetrically minor and do not affect the average density of the pyramid. The density of the Great Pyramid was considered in detail for the micro-gravity measurements of Lakshmanan and Montlucon (1987). Their experimental study was intended to detect the possible presence of undiscovered chambers, which would manifest themselves as a small deficit of gravity values measured within the pyramid. The effective average density of the pyramid was concluded to lie close to 2000 kg m⁻³. The relatively small volume occupied by internal chambers would have a negligible effect on the external gravity field. The pyramid volume using the geometrical measurements would have been roughly 2.6×10⁶ m³ (cf. 2.34×10⁶ m³ of Bui, 2012) and the mass of the pyramid is estimated at 5.2×10⁶ t using the mean density of 2000 kg m⁻³ given by Lakshmanan and Montlucon (1987). The same density has been used here to model the horizontal gravitational attraction. Any calculated deflection of the vertical is proportional to this constant density used for the model.

Had Hutton conducted his desired pyramid deflection experiment, in the early 19th century, the geometry of the pyramid would be much as it is today. Given the bulk of the pyramid, any minor surficial changes or internal voids are unlikely to have had a significant effect on the estimate of the deflection of the vertical on the pyramid's exterior.

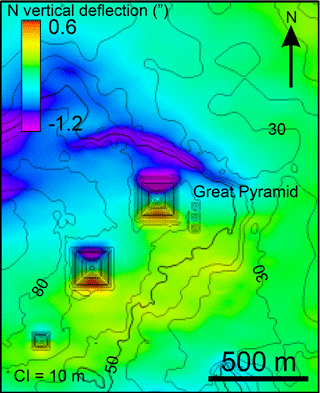
Figure 3 Calculated northward deflection of the vertical (colours) with topographic contours (black) around the pyramids. The highest calculated deflections are on the northern and southern flanks for the bigger two pyramids, though the northern edge of the Giza Plateau also has a strong southerly deflection of the vertical. Densities assumed are 2000 kg m⁻³ for the pyramid and 2200 kg m⁻³ for the topography. Topographic contour interval 10 m.

In addition to the fine-scale gravity measurements of Lakshmanan and Montlucon (1987) inside the pyramid, other modern gravity measurements have been taken on the pyramid's exterior. Small variations in these have been interpreted to indicate the positions within the pyramid of building ramps which are now enclosed (Bui, 2012). The mean density of the pyramid was estimated by Bui (2012) to be about 2050 kg m⁻³, a similar value to that determined by Lakshmanan and Montlucon (1987).

To estimate the effect that Hutton could have measured, the deflection of the vertical (horizontal gravitational attraction) was computed for a complete range of points across the area using a moving circular grid of columns like that which Hutton devised for the Schiehallion experiment. The calculation of the deflection of the vertical has been made both with and without the pyramid to separate the wider topographic effect from that of the man-made pyramid. The density taken for the vertical deflection effect of the topography was a little higher than that for the pyramid, at 2200 kg m⁻³, reflecting a likely modest reduction in porosity with burial.

The maximum deflections of the vertical occur about 85 m from the pyramid crest, as predicted by Hutton (Fig. 3). Inclusion of the surrounding local topographic effect in these calculations shows that there is also a strong (southward deflection) response along the escarpment north of the pyramids (Fig. 3). However, in a similar way that the regional effects have a negligible effect on the differential measurement between the pyramid stations, even the local topographic effects of the Giza Plateau make only a small contribution to the deflection of the vertical that would be measured, as described above.

The modelled north–south vertical deflection is shown in Fig. 3. Stations 85 m north and south of the pyramid crest, as suggested from Hutton's estimate of the position where maximum deflection would occur, would have 5.5 arcsec of geographic latitudinal separation, while the gravity model suggests that an apparent latitudinal separation of 7.3 arcsec would be expected, the addition due to the vertical deflection caused by the pyramid's mass. The total inward deflection of the vertical at the pyramid caused by its mass is 1.8 arcsec (0.0005^∘) in a north–south direction. The southward deflection on the northern side of the pyramid is slightly stronger than the northward deflection on the southern side, as the local topography of the Giza Plateau and other pyramids make a small gravitational contribution (Fig. 2a). Had stations been placed on the eastern and western flanks of the pyramid, and the vertical deflection been measurable in that plane, an inward deflection of 2.0 arcsec would be expected.

Although the 1.8 and 2.0 arcsec effects are small, these quantities would have been detectable by the astronomical techniques developed and the zenith sector used by Maskelyne for the Schiehallion experiment. A digital recreation of Hutton and Maskelyne's Schiehallion experiment in Scotland showed that the historical astronomical measurements were of sufficient accuracy to suggest an Earth density estimate of 5480±250 kg m⁻³, in line with a currently accepted value of 5515 kg m⁻³ (Smallwood, 2007), so with less error arising from the topographic survey, a pyramid experiment may have allowed Hutton to reach a similar value.

5 Discussion

The corollary of the deflection of the vertical measured between the flanks of the pyramid being uninfluenced by long-range regional effects is that the pyramid only has a tangible influence on the gravity field for hundreds of metres, commensurate with its scale (Fig. 2b). This would have been favourable for historical deflection experiments, as a wide topographic survey would not have been necessary. This study shows that Hutton, possibly the most prominent British mathematician of his generation (Wardhaugh, 2017), had indeed suggested a viable method by which the plumb-line-derived Earth density estimate could have been improved.

It might be expected that although smaller than those at Schiehallion, the pyramid's deflections of the vertical of 1.8 and 2.0 arcsec would have been measurable given the zenith sector's resolution, and as at Schiehallion, a number of observations could be averaged. Meteorological conditions would be more benign in Egypt than they had been in Scotland, where conditions were marked by a “badness of the weather” (Maskelyne, 1775b).

Although the modelled vertical deflection was within the detectable range of the instrumentation, techniques to measure Earth's density (and the gravitational constant) were already starting to move away from relying on measurement of deflection of the vertical by a large mass such as a mountain, or indeed a pyramid, in Hutton's time. In 1798, Henry Cavendish, perhaps assisted in his motivation by his discussions with Hutton on estimating plumb-line deflection from topography (Hutton, 1778), published his torsion-balance-determined Earth density estimate of 5480±33 kg m⁻³ (Cavendish, 1798). This determination, stemming from Newton's alternative suggestion for demonstrating gravitational attraction, was close to the currently recognized value, and stood for some time, though an arithmetic correction of those experimental results was subsequently made to 5448 kg m⁻³ by Francis Baily in 1821 (Poynting, 1894). What has become known as the Cavendish experiment was so carefully designed and executed, and conditions much more controlled, that it seems rather unlikely that any plumb-line deflection experiment (e.g. James, 1856 on Arthur's Seat in Edinburgh) even on a geometrically regular structure like one of the pyramids, would have improved upon Cavendish's result for Earth's density. Early plumb-line and torsion balance Earth density estimates have been compiled by Hughes (2006) who noted that from early to mid 19th century times, torsion balance determinations “consistently gave the best results”. This has been borne out by recent gravity studies at the Great Pyramid, which have been motivated by more local interest in detecting possible internal cavities than by a desire like Hutton's to improve the Earth density estimate.

6 Conclusions

The modelled summed inward vertical deflection is 1.8 arcsec between the northern and southern flanks of the pyramid and 2.0 arcsec between the eastern and western flanks. Hutton could be reassured that these deflections would have been measurable by his contemporaries, and Maskelyne placed suitable confidence in his zenith sector. The Schiehallion Earth density estimate might indeed, therefore, have been improved upon at the Great Pyramid, though the technique is not preferable to a torsion balance method to estimate Earth's density. In spite of the physical challenges accompanying the occupation of exposed observatories and inclement weather, Maskelyne was able to use his zenith sector to successfully record a subtle vertical deflection effect on Schiehallion, and it could be expected that the experiment at Giza suggested by Hutton could have yielded an improved Earth density quantity without a geographically wide topographic survey.