On the high scientific quality of early research on strain and deformation fabrics (1835–1908)

High-quality research developed during the 19th century established the foundations of rock strain investigations. Careful observation and description of rock fabrics and deformed objects in rocks allowed early researchers to obtain mathematical expressions that are still used today to quantify strain. Thus, in a span of a few decades, and applying basic scientific methodology, these researchers developed the concept of the strain ellipsoid, defined mathematically the difference between constant-volume and volume-loss deformation, constructed the basic equations that define pure and simple shear deformation, and discovered the mechanism of pressure–solution deformation. These advances were fundamental to seminal works on strain analysis and deformation fabrics in the mid-20th century. However, they are rarely addressed in modern studies, which suggests a lack of awareness among current researchers. In order to bring attention to these landmarks of strain research, I provide a historical review of the high standards of analysis that led to the definition of the fundamental equations and concepts on strain during the 19th century.

1 Introduction

During the 19th century, a number of researchers realized that some rocks provide excellent insights into their deformation history. Aside from folds, the most notorious evidence of deformation, these rocks bore constituent objects such as fossils or some minerals that were also deformed. In those rocks in which metamorphism was not so intense, the finite strain state could be determined, and a relationship between this state and the deformation fabrics, such as fractures and cleavage, could be discussed. This discussion was very prolific, and its legacy included a great deal of accurate observations and deductions that led to the assemblage of the fundamental equations on which we base our present understanding of rock strain.

Further developments on strain during the first part of the 20th century were strongly based on these older studies. Many of them were reviewed by structural geology textbooks between the 1960s and 1970s (De Sitter, 1964; Ramsay, 1967; Hobbs et al., 1976), leading to novel techniques of strain analysis (e.g., Ramsay, 1967; Ramsay and Huber, 1983, 1987). In the last 40 years, introduction of advanced computing, statistical methods, and simulations, as well as techniques of electron microscopy, geochronology of mineral phases involved in deformation, and anisotropy of magnetic susceptibility, among other techniques, have resulted in significant advances in the field (Hobbs, 2019; Wenk et al., 2020; McCarthy et al., 2020). However, a simple search in citation repositories of some of the more fundamental papers from the 19th century shows a scarce acknowledgement of them in the last 15 years (between zero and three citations per year, most of them incidental). As pointed out in a recent volume celebrating 50 years of John Ramsay's book, Folding and Fracturing of Rocks (Bond and Lebit, 2020), much of the research developed in the last decades and in this book applied strain analysis techniques to perform mathematical models of rock deformation. However, many definitions and findings put forward by Ramsay (1967) and other contemporary researchers (Cloos, 1947; Breddin, 1955; Galvin, 1959; Elliott, 1970, among others) were based on mathematical contributions settled during the previous century. There have been some important historical reviews of the development of concepts relating to deformation fabrics, such as cleavage or cataclastic rocks (e.g., Higgins, 1971; Siddans, 1972), but I think that a thorough review of the significant conceptual definitions and mathematical improvements made in that early research is lacking and will help to put into perspective their fundamental contribution to our current knowledge on strain.

In this paper I make a review of the timeline of development of fundamental concepts regarding strain studies in the 19th century. I will emphasize the quality of these early studies, with focus on the main landmarks regarding the definition of concepts that persist today (with slight terminology or conceptual modifications) and the accurate mathematical reasoning and precise observations that established the foundations of the more modern strain analysis techniques developed during the last century. Hopefully, this contribution will help to give due visibility to papers that are usually neglected, with the only excuse of a lack of awareness, since at present they are largely available in electronic format.

Table 1 Explanation of symbols used in the text and list of terms used in the revised bibliography with their modern equivalents.

2 The association of cleavage and finite strain

During the first decades of the 19th century, a slate was defined in textbooks, such as Bakewell (1813), as a “transitional rock” (between primary and secondary) that could be split into thin laminae, which were often used as roof slates. This capacity to split was referred to as cleavage by British geologists, but aside of its usefulness to construct roofs, its importance as a record of rock structure remained poorly understood until Adam Sedgwick, in 1835, published the first scientific study on the subject. Sedgwick (1835) emphasized the distinction between cleavage, stratification, and jointing (pp. 471–472, 480) and noticed the continuity of the strike of cleavage across large areas and its general parallelism with the strike of bedding. Sedgwick, however, suggested that cleavage was the result of chemical action (“crystalline forces”) and disregarded its connection with mechanical processes (p. 481). He based his conclusion on the notorious parallel arrangement of flaky minerals (e.g., chlorite and mica) “which not merely define the planes in question but strike in parallel flakes through the whole mass of the rock” (p. 471). Nevertheless, it is very interesting that he ascribed these chemical changes in slates to metamorphism, comparing these rocks to mica schists. Charles Robert Darwin (1846) also interpreted that the “power” that formed cleavage in slates “has tended to modify its mineralogical character in parallel planes” and that “in most cases foliation and cleavage are parts of the same process” (metamorphism); “the foliation [of schists and gneiss] is the extreme result of that process, of which cleavage is the first effect” (pp. 163–167). This was later also supported by Sharpe (1852) upon observations in northern Scotland, although neglecting metamorphism as the cause.

In 1844, John Phillips reported his observations on the internal structure of rocks and reaffirmed the concept of cleavage parallel to “the great anticlinal axes” (Phillips, 1844, p. 61), an observation comparable to Sedgwick (1835) regarding parallelism of bedding–cleavage strike. This was also emphasized by Darwin (1846) from observations in the southernmost Andes, where cleavage strike is parallel to the “main axes of elevation” (pp. 162–163) (see Table 1 for modern terminology), and later by Rogers (1857), who included the concept of folds' axial planes to which cleavage is parallel. Phillips was among the first to notice that fossils were deformed in the slates, what he considered the result of a “creeping” along cleavage planes; but more importantly he envisaged the usefulness of measuring the distortion of fossils as one of a series of steps towards a mechanical theory of rock deformation.

This line of thought was more or less contemporaneously faced by Daniel Sharpe (1847), who published the first detailed analysis on the relationship between distorted fossils and cleavage formation, emphasizing the mechanical nature of this relationship. Sharpe's observations led him to this premise: “if we could find out that the changes of form in the [fossil] shells followed any certain law we might make allowance for them and thus discover the original form of the shell” (p. 75), a statement of the rationale of practical strain determinations from deformed objects! He continued: “the impressions of several shells (…) were all distorted in the same direction; the change having no reference to the original figure of the shells, but to their position on the stone: it appeared as if every specimen had been contracted in the same direction”. This direction, he found, was perpendicular to the orientation of the cleavage planes, and the amount of distortion was proportional to the degree of cleavage development. In addition, he also observed that the fossils were stretched parallel to the cleavage dip and assumed constant-volume deformation: “the compression of the mass between the cleavage planes has been counterbalanced by its expansion in a direction corresponding to the dip of the cleavage” (p. 81). If any geologist has asked himself how the concept of strain has been at some moment related to penetrative rock fabrics, reading Sharpe's paper will give the answer.

Sharpe (1849), in a second communication on slaty cleavage, extended his research to non-fossiliferous slates. He found evidence supporting his previous conclusions, which we may call by its modern name: strain markers. In this case the markers were imbedded clasts (“pebbles or fragments”) in slaty breccias, with their flattest sides parallel to cleavage planes. Sharpe concluded that this flattening was due to shortening perpendicular to cleavage, since the clasts' long axes were occasionally found normal to bedding (if bedding and cleavage were normal), thus in “a position which they never could have reached if their forms had been originally those we now find” (p. 112). He further related the forces causing shortening to “the elevation of great masses of rock under conditions of which we are ignorant”, giving a tectonic interpretation of his results (pp. 128–129).

Using magnification, Sharpe observed that in the finer slates the constituent particles were also “flattest between the cleavage planes and longest along the dip of the cleavage” (p. 113). He arrived at the conclusion that the property of slates of splitting in a preferred direction (i.e., the cleavage) was a secondary character caused by the preferred orientation and shape of their deformed constituent particles. Accordingly, “the rock can offer less resistance (…) down the plane of cleavage (…), than in any other direction; for that plane (…) pass along the flat surfaces of many of the particles and intersect a smaller number of them than any other plane” (p. 114). In addition, he put forward the first detailed description of what we know now as cleavage refraction, which he attributed to “beds of different hardness offering different degrees of resistance to pressure” (p. 118), i.e., a purely mechanical origin.

3 The development of strain measurement techniques

Another pioneer in the study of rock strain, Henry Clifton Sorby, published in 1853 the results of his study on the origin of slaty cleavage based on observations in the field and on thin sections. In this later methodology he was definitely leading. He corroborated the conclusions of Phillips (1844) and Sharpe (1847, 1849) on the relationship of cleavage to shortening, both in orientation and intensity. Sorby used a different kind of strain marker: folds. By studying their geometries and relationships to cleavage, he found the coincidence between cleavage and the axial surface of folds and concluded that they indicated a “considerable amount of lateral pressure”, with bed thickness changes between limbs and hinges indicating elongation parallel to cleavage and shortening perpendicular to it (Sorby, 1853, p. 138). While describing the geometry of disharmonic folds (“contortions”) on sandy beds in shale, he applied bed-length balancing to conclude a shortening of 75 %, which in the shaly matrix was accommodated “by absolute forcing together of their ultimate particles, but also by elongation in the line of dip of cleavage” (p. 139), i.e., by a change in dimension of the rock.

Adding to his observations, Sorby analyzed the change of shape of “green spots” in slates, which are concretionary forms that in the undeformed state are either spherical or ellipsoidal, with elongation in the bedding plane (i.e., with an original shape fabric). When deformed, the spherical varieties attained an ellipsoidal shape, with the long axis parallel to the cleavage dip and the shortest axis perpendicular to it, while in the cases of an original shape fabric, the long axes were positioned intermediately between cleavage and bedding. These observations reinforced the theory of shortening perpendicular to cleavage planes.

From his study of deformed ellipsoids, Sorby arrived at interesting conclusions regarding constant-volume plane strain deformation: using simple mathematic calculations and numerous measures of deformed green spots, he obtained the mean ratio between the three ellipsoid semiaxes $a>b>c$ and found that in the plane perpendicular to cleavage, the ratio $a/c$ was more than 2 times larger than expected for constant-volume plane strain deformation of an original sphere (where b is equal to the initial sphere radius, and $a/c=a^{\mathrm{2}}/b^{\mathrm{2}}$). This meant an excess shortening of 57 % parallel to c. Even if this amount is considered rather large, he concluded that the studied slates had reduced their original volume to one-half, due to “the forcing of the particles more closely together, so as to fill up the spaces left between them (…); their very close packing, as seen in thin sections, agrees well with this supposition” (Sorby, 1853, p. 142).

While describing slates under the microscope, Sorby underlined the preferred orientation of micas and other non-equiaxed particles (e.g., sand grains, shells and coral fragments) at angles close to the cleavage planes and argued that this fabric constituted a structural weakness responsible for the “fissile character” of slate. This led him to develop the equation that gives the final angle φ^′ of randomly distributed lines (non-equiaxed particles in a rock), with respect to the extension direction, when the initial angle φ and the strain ellipse ratio R are known (see Appendix A):

$$\begin{array}{}\text{(1)}& \tan \mathit{\phi }{}^{\prime }={\displaystyle \frac{\tan \mathit{\phi }}{R}}.\end{array}$$

This equation demonstrates that the final angle of the long axes of these particles will be closer to the most stretched axis of the ellipsoids (the cleavage dip direction) after deformation (Sorby, 1853). Sorby also tested his theoretical predictions with analog experimentation, being also a pioneer in this subject. He mixed scales of iron oxide in clay to imitate randomly oriented micas in shale, compressed the mixture, and baked it and obtained the predicted results: the scales did rotate and attained a preferred orientation perpendicular to the applied force.

Sorby's observations under the microscope were of such a quality that he even described what would later be called strain shadows:

On each side of the larger rounded grains of mica, in the line of cleavage, in well-cleaved slates, the particles are arranged evenly at all angles, over small triangular spaces, having their bases towards the grain. This is just the part which would be protected from change of dimensions by its presence [by the larger mica grain]; and this fact is therefore very good evidence of the slate having had originally such a structure [random orientation of micas]. (Sorby, 1853, p. 145)

Sorby further noticed, like Sharpe, the relationship between cleavage intensity and magnitude of strain and also the characteristic refraction when crossing beds of different competency. He deepened the mechanical explanation of this phenomenon, which he correctly associated with the different rheology of each layer, evidenced, for example, by the fanning out of cleavage in shaly horizons when approaching the convex surface of an anticline in a sandy layer and the cleavage fans developed in the competent beds. When explaining his theory for refraction, he realized that the different amount of deformation on each bed is inexistent along the bedding plane; in his words, “the amount of elongation in the line of dip [of bedding] could not vary” (since no detachment was observed; Sorby, 1853, p. 145). Therefore, the shale can accommodate more contraction (with volume loss) than the sandstone only in a direction normal to bedding, resulting in a cleavage plane more inclined towards the interface (Fig. 1). We will see how Harker (1886) further explained this concept, but still Sorby's theory remained as one of the possible explanations for strain refraction in multilayers: the difference in bedding–normal compaction across the surface (Ramsay and Huber, 1987).

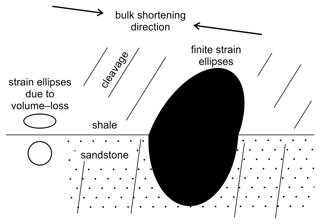
Figure 1 Graphic representation of Sorby's ideas (Sorby, 1853) on the superposition of the deformation caused by volume loss (only possible normal to bedding) on the deformation due to general shortening of the rock and how this causes different but compatible finite strain ellipses in each lithology. Cleavage parallels the finite strain ellipses, being thus refracted. Figure based on Ramsay and Huber (1987, Fig. 21.24).

It is also interesting that Sorby (1853) underlines the occurrence of a “linear graining (…) due to small puckerings of the [schist] beds and may be called plications of the first order” (p. 147). He observed the regional parallelism of these “plications” with the strike of cleavage in slates and of larger fold axes. This may be one of the first descriptions of crenulation lineation in the literature. He also compared the movements and changes in dimensions of rocks predicted by his theory with the slow flow of other solids, such as glacier ice and brittle pitch.

One of the most important contributions of Sorby to our present knowledge of strain is the introduction of the most elemental two-dimensional expression of rock deformation: the strain ellipse. This was done almost contemporaneously with Samuel Haughton, who applied the principle to three-dimensional deformation (deformation ellipsoid). Both researchers published their results in the same volume of the Philosophical Magazine, with months of separation, in 1856. Although he did not call it by its present name, which will be used for the first time more than 20 years later (see Siddans, 1972), Sorby (1856) defined the strain ellipse principle as follows:

If a rock has not been compressed, we may express this by saying that the ratio of the alteration in any two directions at right angles to each other is as 1:1; whilst if it had been compressed in such a manner that the proportion between lines of equal length before compression was changed so that in the line of pressure the length was one-sixth of that perpendicular to it, we may say that the ratio is as 1:6. If, for instance, before compression we had a circle, afterwards it would be an ellipse, whose axes were as 1:6. (p. 27)

Going further with his study of deformed objects in cleaved rocks, Sorby (1856) described deformed encrinites in which the crinoid ossicles (“joints of encrinites”) were distorted as a result of shortening perpendicular to cleavage and extension parallel to its dip, with an axial ratio (a :c) of 4:1. He also described the distortion of calcite crystals in slaty limestones (broken crystals, bent cleavage), interpreting this as deformation without need of heat, “by the gradual movement of the ultimate atoms one over the other” (p. 33). This deformation caused the following:

The crystalline granules have a very unsymmetrical character, having their axes in the plane of cleavage very much longer than perpendicular to it, as though the compression indicated by the joints of the encrinites and larger crystals had affected the smallest, constituting the ultimate structure of the rock. (p. 34)

Again, the interpretation for cleavage is that the line of weakness in such a rock would be along the longer axes of the deformed crystals and ossicles, i.e., perpendicular to the maximum shortening.

Haughton (1856) made another brilliant contribution to the study of rock strain by contrasting the mechanical theory of cleavage formation by “accurate numerical investigation”. His work, therefore, stated a firm basis for further theoretical development. Haughton collected and measured a great number of deformed fossils and analyzed them under a similar rationale to Sharpe (1947):

Each species of fossil has a certain normal undistorted form which may be ascertained, and (…) the measurements of the different parts bear, within certain narrow limits, a constant ratio to each other; so that when we examine a distorted fossil, we can calculate the amount of relative extension or compression it has undergone in any direction. (Haughton, 1856, p. 410)

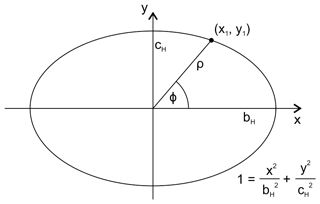
Haughton developed the concept of Cauchy's ellipsoid of distortion to understand rock strain. I will treat his deductions in detail since they are relatively simple and give good results, considering the premises. Among these, the strain ellipsoid is assumed to be with a_H (major semiaxis) parallel to the cleavage–bedding intersection (the suffix “H” is used to differentiate from the semiaxes of the ellipsoids considered by later authors and in modern notation, where a_H=b), c_H (minor semiaxis) perpendicular to the cleavage plane, and an intermediate semiaxis, b_H, parallel to the cleavage dip. The intersection of this ellipsoid with any plane parallel to a_H (e.g., bedding) is an ellipse, whose semiaxes are ρ and a_H, parallel to the dip and strike of the plane, respectively (Fig. 2a, b). The ratio $\mathit{\rho }/a_{\mathrm{H}}$ is the distortion (or axial ratio, in modern terminology) parallel to the dip direction, whilst $a_{\mathrm{H}}/\mathit{\rho }$ is the distortion parallel to the strike. Haughton assumed a_H to be equal to unity in his equations; thus the former ratio would be just ρ and the latter ρ⁻¹. However, as discussed by Harker (1886; see below), this condition is not widely verified in nature, so it is better to use the general forms.

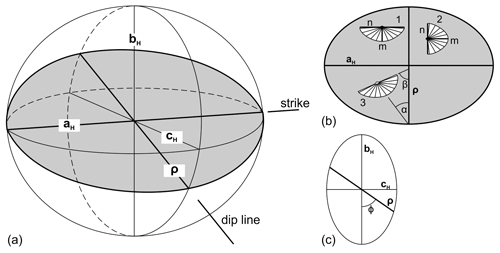
Figure 2 (a) Strain ellipsoid of Haughton (1856), intersected by a bedding plane (gray shaded) with strike parallel to a_H and dip direction parallel to the b_Hc_H plane. (b) Plane view of the bedding with examples of deformed fossils of length n and breadth m. (c) Section of the strain ellipsoid across the b_Hc_H plane.

If we consider the ellipse formed by the intersection of the strain ellipsoid and a plane parallel to b_Hc_H and the intersection of this plane with the one containing ρ (Fig. 2c), it follows from the equation of the ellipse that the relationship between ρ and the semiaxes b_Hc_H is

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}^{\mathrm{2}}}}={\displaystyle \frac{{\cos }^{\mathrm{2}}\mathit{\varphi }}{b_{\mathrm{H}}^{\mathrm{2}}}}+{\displaystyle \frac{{\sin }^{\mathrm{2}}\mathit{\varphi }}{c_{\mathrm{H}}^{\mathrm{2}}}},\end{array}$$

where ϕ is the angle between the plane containing ρ and the b_H semiaxis (Fig. 2c). If we use axial ratios to a_H ≠ 1, we obtain the more adequate general form (cf. Harker, 1886)

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}}{{\mathit{\rho }}^{\mathrm{2}}}}={\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\varphi }}{b_{\mathrm{H}}^{\mathrm{2}}}}+{\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\varphi }}{c_{\mathrm{H}}^{\mathrm{2}}}},\end{array}$$

which allows us to determine the distortion $\mathit{\rho }/a_{\mathrm{H}}$ in any plane making an angle ϕ with cleavage (the a_Hb_H plane). If these planes of interest are bedding planes, and we find two (with angles ϕ, ϕ^′) on which we can calculate the distortions $a_{\mathrm{H}}/\mathit{\rho }$ and $a_{\mathrm{H}}/{\mathit{\rho }}^{\prime }$, then we can determine the ratios of the axes of the strain ellipsoid with the following equations, which result from working out Eq. (3) in each case (see Appendix A):

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{a_{\mathrm{H}}}{b_{\mathrm{H}}}}={\left[{\displaystyle \frac{\left(\frac{a_H\sin \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}+\frac{a_{\mathrm{H}}\sin {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}\right)\left(\frac{a_{\mathrm{H}}\sin \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}-\frac{a_{\mathrm{H}}\sin {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}\right)}{\sin \left(\mathit{\varphi }+{\mathit{\varphi }}^{\prime }\right)\sin \left(\mathit{\varphi }-{\mathit{\varphi }}^{\prime }\right)}}\right]}^{\frac{\mathrm{1}}{\mathrm{2}}}\text{(5)}& {\displaystyle \frac{a_{\mathrm{H}}}{c_{\mathrm{H}}}}={\left[{\displaystyle \frac{\left(\frac{a_{\mathrm{H}}\cos {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}+\frac{a_{\mathrm{H}}\cos \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}\right)\left(\frac{a_{\mathrm{H}}\cos {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}-\frac{a_{\mathrm{H}}\cos \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}\right)}{\sin \left(\mathit{\varphi }+{\mathit{\varphi }}^{\prime }\right)\sin \left(\mathit{\varphi }-{\mathit{\varphi }}^{\prime }\right)}}\right]}^{\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

To obtain the distortions $a_{\mathrm{H}}/\mathit{\rho }$ and $a_{\mathrm{H}}/{\mathit{\rho }}^{\prime }$, Haughton used the ratios between pairs of orthogonal lines in undeformed fossils, for example, length and breadth (lines M and N), which remain orthogonal in deformed fossils (m and n) (symmetric fossil forms; cf. Ramsay and Huber, 1983). For this condition to be met, one line should be parallel to a_H and the other parallel to the dip of bedding (direction of ρ) (Fig. 2b, fossil forms 1 and 2). If, for example, m is parallel to ρ (fossil 1 in Fig. 2b), the distortion in the bedding plane is

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathit{\rho }}{a_{\mathrm{H}}}}={\displaystyle \frac{m}{n}}{\displaystyle \frac{N}{M}}.\end{array}$$

If m is parallel to a_H (fossil 2 in Fig. 2b), the same equation gives $a_{\mathrm{H}}/\mathit{\rho }$ for that bedding plane. In Haughton's examples, a_H is considered unity; therefore by Eq. (6) we would obtain the linear strain (stretch) parallel to m. He applied this methodology to deformed brachiopods and trilobites and obtained the axial ratios of the strain ellipsoids, which indicate a majority of nearly oblate shapes. He found others that showed a greater amount of distortion, however, such as the same brachiopods described by Sharpe (1847), with a mean axial ratio of $\mathrm{1}:\mathrm{0.669}:\mathrm{0.102}$ (long axis horizontal). From this quantitative approach, Haughton (1856) could also appraise the different intensity of shortening and degree of cleavage development in sandstones, which showed the less distorted fossils, concluding the following:

Sandstones resist the cleavage action or pressure better than slate or mud. This singular fact, of a less compression existing in sandstones than in slates, and a proportionably less-developed cleavage, is a solid argument in support of the mechanical theory of cleavage. (pp. 417–418)

Haughton also challenged Sharpe's observation of “an expansion parallel to the cleavage dip and no change in the direction of strike”. He suggested that these were generalizations, since no data existed on the “absolute compression or expansion undergone by the rock in any direction” (p. 420).

4 A preliminary classification of cleavage

In the following years, Sorby (1858) made new original contributions to the study of cleavage, as always based on careful observations and measurements. He distinguished, for the first time, between two particular types of cleavage that represent the ancestry of the modern morphological classification between continuous and spaced cleavages (or foliations) (see Gray, 1977; Powell, 1979). These types, as defined by Sorby (1858), were “ultimate-structure cleavage” (continuous cleavage), which is the one present in the slates used for his studies on strain, that “would result from the rock yielding to pressure as a plastic substance”, and “close-joints cleavage” (spaced cleavages), due to very close partings (joints) that are “often so close as to be quite undistinguishable unless a thin section is examined with the microscope”. The spaces between these cleavage planes (microlithons in modern language) have an independent fabric, which may be related to other planes (e.g., bedding). He mentions, although gives no detail, experiments on which this kind of cleavage would result from the rock being subjected to a “change of dimensions like a rigid body, by the formation of close cracks”. Although he initially did not clarify the kinematic nature of these cracks, many later researchers and Sorby himself assumed them to be shear fractures.

It is most interesting that a concluding remark on this distinction of cleavage types suggests their utility to indicate differences in rheology during deformation and also differences in strain rate:

These two kinds of cleavage obey materially different laws; but at the same time, in like manner as there is a gradual passage from rigidity to plasticity, so there is also between these two kinds of structure (…); and thus the structure affords an indication of the actual condition of the rocks at the time when they were compressed and perhaps also, in some cases, indicates whether the movements of elevation were sudden or gradual. (Sorby, 1858, p. 93)

5 The pressure–solution paradigm

Some years later, Sorby (1863a) published another paper in which he described the correlation of “mechanical and chemical forces”. The more important geological outcome of this research was that he started to envisage the importance of pressure in the increase or decrease of solubility of some minerals and its influence on the creation of cleavage:

A number of facts connected with metamorphic rocks and the phenomena of slaty cleavage (…) are readily explained if mechanical force be directly correlated to chemical action, and if in some cases the direction in which crystals are formed be more or less related to pressure. (p. 549)

These first ideas were developed in more depth in two subsequent papers (Sorby, 1863b, 1865), in which the study of limestone pebbles penetrating into one another (impressing each other) showed that it was possible to “produce chemical changes by mechanical pressure” (Sorby, 1865, p. 460). His observations showed that the impressions “were produced by the actual removal of material and not by its yielding as a plastic substance”, and while the soluble material was removed, “the insoluble earthy portion [was] left behind at the bottom of the depressions” (p. 460). He concluded that “striking examples are met with in the case of rocks affected with slaty cleavage” (p. 461). As was expressed by Durney (1978, p. 370), Sorby “had discovered pressure–solution, although he did not give the process this name until 1908”.

From this point, Sorby incorporated the action of pressure–solution into his mechanical theory of cleavage, at least in calcareous rocks. A beautiful example of his understanding of rock strain is given in a paper published in 1879, in which he describes a deformed limestone band from Ilfracombe, reproduced in Fig. 3a (his Fig. 10). The description states the following:

[A thin limestone band] has been bent up into a number of contortions, though the upper and lower beds are not contorted, no doubt because they yielded to the pressure as plastic substances, whereas the calcareous band did not so yield. Though no doubt the band was originally of nearly uniform thickness, (…) the carbonate of lime has been entirely removed where it would be nipped [squeezed] between two other portions of hard limestone, and thus exposed to the full effects of pressure, whilst it remains where it would be relatively protected from pressure, at the curved ends of the contortions. (…) It would, I think, be difficult to find a better illustration of the influence of mechanical pressure on solvent chemical action, (…) showing, as it does so clearly, that solution has taken place where there was great pressure and stress, and deposition where they were relatively less. (Sorby, 1879, pp. 88–89, italics are mine)

Emulating Durney, we could say that Sorby had discovered rootless folds and transposition cleavage, without giving the names.

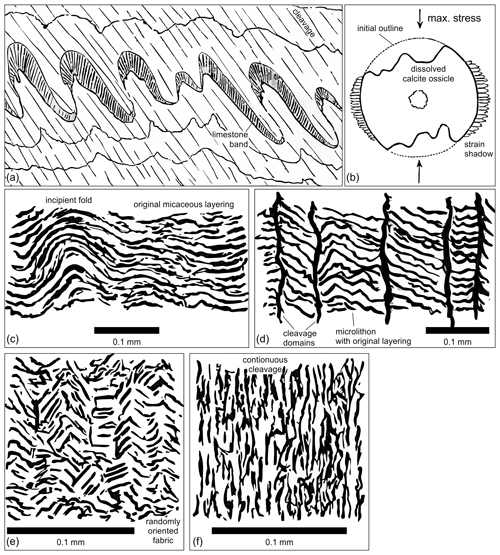
Figure 3 (a–b) Figures redrawn from Sorby (1879), no scale in the original (see original description in text). (a) Folded limestone band from Ilfracombe, in which Sorby described rootless folds and transposition cleavage, formed by pressure–solution along folds' limbs. (b) A crinoid ossicle seen under the microscope, with dissolved edges and calcite fibers in the strain shadows and with the interpreted direction of maximum stress. (c–d) Figures redrawn from Sorby (1880), showing the progressive deformation of a slate. Textual captions between brackets (see text for original description). (c) “Slate, Liskeard, with minute contortions”; the fine micaceous sedimentary lamination is deformed into open or gentle microfolds. (d) “Slate, Liskeard, with planes of discontinuity”; further contraction causes the formation of an imperfect cleavage, in which Sorby recognized the concentration of oxides. (e) “Slate, Shap, disturbed by pressure”; in this case the first stage does not develop gentle folds, instead disturbing the original layers into a randomly oriented fabric with possibly minor kinks. This may also be the case of a rock without a clear primary fabric. (f) “Slate, Llanberis, with well–developed cleavage”; this final stage shows a continuous cleavage developed under higher deformation.

In addition to this face evidence, Sorby confirmed his interpretation under the microscope (Fig. 3b) (his Fig. 11):

Some joints of Encrinites [crinoid ossicles] have been dissolved and their outline altered from the original (shown by the dotted lines) and mutually penetrate when in the direction of pressure (shown by the arrows), whilst the dissolved material has crystallized out on each side where more protected. (Sorby, 1879, p. 89)

This effect, he states, has also been observed in uncleaved limestones where it is due to the “pressure of superincumbent strata”.

A few years before, Edward Hitchcock put forward new evidence of the effects of ductile deformation on sedimentary rocks, from his studies in the Purgatory Conglomerate of southern Rhode Island, in the United States (Hitchcock, 1961). He reported that the clasts of this conglomerate were highly flattened and, especially, elongated, with the maximum stretch parallel to the regional structural trend. He pointed out that the clasts were “indented often deeply by one being pressed into another” (p. 374), which is a feature similar to that Sorby would describe from his impressed pebbles (Sorby, 1865). Hitchcock intuitively concluded that the clasts should have been in a “plastic state” in order to allow for their shape change, since in their current, non-plastic state, “the attempt to change their present form would result only in fracture and comminution” (Hitchcock, 1961, p. 375).

6 Early developments of progressive deformation models

Sorby (1880) also contributed to the description of non-calcareous rocks and highlighted his observations on the origin of cleavage in these rocks. Building on theories briefly presented in 1858, and upon observation of numerous thin sections, as well as improved optical techniques, he revised his interpretation on the origin and significance of mica in slates and therefore on the origin of cleavage on micaceous slates and schists. He considered, thus, that mica in slate is detrital, “derived from the disintegration of an older rock” such as “fine-grained micaceous felsites” (Sorby, 1880, p. 70). This argument, however, led to the problem of an original fabric in the undeformed rock, namely the fine lamination of micaceous mudstones, which would lack the randomly oriented non-equiaxed particles used by Sorby in his initial theory for cleavage formation (Sorby, 1853). In his words, “I had never found any uncleaved slate rock having now the exact structure which I assumed that the cleaved rocks had originally” (Sorby, 1880, p. 72).

Thus, while examining several thin sections to compare slates with different degrees of cleavage development, Sorby again found the two types of cleavage mentioned in his paper from 1858: ultimate cleavage and close-joints cleavage; and he put forward a theory that relates both in a progressive deformation scheme. In Fig. 3c–f, we reproduce his figures 3 to 6 (from Sorby, 1880), where this progressive deformation is illustrated. An imperfectly cleaved slate shows a very fine sedimentary lamination, formed by the parallel arrangement of minute mica flakes, which after an amount of contraction is deformed into open or gentle microfolds (Fig. 3c). “Such a rock could yield in this manner only to a very moderate extent without the contortions breaking and the detached portions moving one over the other, so as to give rise to a system of approximately parallel planes of discontinuity or close joints” (p. 72) (Fig. 3d). The resultant cleavage is an imperfect one, “due to the lateral yielding of a rock composed of material not truly plastic in its ultimate constitution” (p. 73). Notably, Sorby observed that the original laminated fabric favored the development of this type of cleavage and that “the joints are still further marked by the subsequent introduction of black oxide of iron”, which leads towards the idea of pressure–solution seams. In other cases, the mica flakes may be “thrown out of their original position” without the development of contortions, resulting in a broken primary fabric that leaves the mica flakes randomly oriented (Fig. 3e). “Further yielding of the rock would totally efface all evidence of the first stages of the process and cause the constituent laminae to become approximately parallel to one plane” (Fig. 3f). This later stage corresponds to the ultimate cleavage type or continuous cleavage in modern terminology. The passage from the state of Fig. 3e to f thus concurs with his initial theory of reorientation of randomly oriented particles during deformation (Sorby, 1853).

Studying the relationship between slates and mica schists, Sorby (1880) described the development of what he calls “cleavage foliation”, formed by crystallization and recrystallization of metamorphic minerals (especially mica and quartz) along the prior cleavage planes (see also Forbes, 1871). He relates this to the model of Fig. 3c–f, citing for example that along the “planes of discontinuity” of Fig. 3d, large “crystals of mica have grown, with their faces and cleavage parallel to the walls”. In some samples of this type “the mica, thus formed along the planes of cleavage discontinuity, increases in amount until, in some parts, it altogether preponderates over the contorted laminae which are roughly parallel to the bedding, and we see a foliation due to large plates of mica lying in a plane corresponding to true slaty cleavage, inclined at a high angle to the stratification”. When this cleavage is perfectly developed, it is “not only parallel to the axis planes of the larger contortions but has all the other characteristic relations of true slaty cleavage” (p. 90). I want to emphasize here how valid this model of evolution of cleavage in progressive deformation and metamorphism still is, which with the simplification given by time is usually found in current textbooks (Twiss and Moores, 2007, pp. 411–413).

Once the study of the “mountains under the microscope”, as inspired by Sorby, caught researchers' attention, further contributions started to put forward more evidence regarding the relationship of cleavage with pressure–solution and transposition of the original fabric of sedimentary rocks. Thomas George Bonney (1884) made some interesting observations on that matter. In studying thin sections of slates cut perpendicular to cleavage, he described a “moderately clear, finely granulated ground mass, divided into minute lenticular streaks by dark lines of variable thickness (…) which are parallel with the cleavage planes [and] are due to the presence of carbonaceous matter, perhaps graphite, with probably some iron oxide” (p. 17). In addition, Bonney described a “pressure structure in banded rock”, which he details as being due to the obliteration of bedding, causing a “new and more conspicuous structure (…) which is parallel to the planes of cleavage” (p. 19). This structure, which we may call transposition cleavage, was described by Bonney as follows:

The more gritty bands are squeezed out into long lenticular streaks, as if the bedding coincided with the cleavage. Where the gritty bands are broadest, there the ends are all “frayed out” (…); where the banding has been fine and rather close, there it has been entirely obliterated and replaced by this new structure of parallel lenticular streaks or elongated “eyes”. (p. 20)

Bonney remarks the importance of this structure for the following reason:

If the action of heat, pressure, and alkaline water (…) had been sufficiently prolonged, we can hardly doubt that the darker laminae would have been converted into bands of mica, the greyer streaks into lenticular aggregates of quartz and feldspar. All trace of the original bedding might thus have been lost, and the presumption from the general aspect of the foliation would have been that the original stratification had been parallel to it. (p. 21)

7 Shearing versus compression

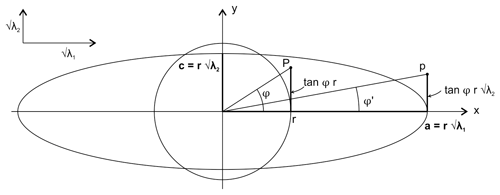
Between 1884 and 1885, a most interesting discussion arose between Osmond Fisher and Alfred Harker in the pages of the Geological Magazine. Fisher (1884a) proposed that the rock strain associated with cleavage, including a flattening perpendicular to cleavage and a lengthening parallel to its dip, was the result of “a pressure combined with a shear” (p. 269), which would explain the lineations parallel to the cleavage dip often seen in slates. He illustrated this concept with his Fig. 1 (reproduced in Fig. 4a), which is the first diagram of simple shear applied to rock strain that I have record of. He argued that this shear was due to the “sinking” of an elevated region after folding (cf. Sharpe, 1847; Phillips, 1857) and showed mathematically how vertical movements of the crust would generate velocity differences in adjacent portions of rock, causing “viscous shearing, without separation of the rock along the surfaces of shear” (p. 273). According to his view, this was the cause of cleavage.

Four months later, however, Fisher modified a part of his theory in a second communication. Here, apparently following a suggestion by Harker, he inquired “whether the greater diametral plane of the ellipsoid of distortion may not be the cleavage plane” (Fisher, 1884b, p. 398), while he previously had considered the cleavage plane a plane of shear. He then compared the diagrams of distorted spiriferids of Sharpe (1847) with the geometry of the strain ellipse resultant from a simple shear and concluded that “the plane of cleavage, therefore, does not lie in the direction of movement among the ultimate particles of the rock but is inclined to it (…) the two directions may become nearly, though never quite, identical as the shear is increased”. Further on, the ellipse “will have two diameters which are equal to the diameter of the circle. One of these will be in the direction of the shear and the other similarly situated on the other side of the minor axis. Objects found along these diameters will not be distorted, while those lying nearer to the major axis will be lengthened and those nearer to the minor shortened” (Fisher, 1884b, p. 400).

According to the observation that cleavage should have formed after folding, Fisher explained the near-parallelism of folds' axial surfaces and cleavage by interpreting the folds to be further distorted, by his simple shear model, after initial formation. This would explain cleavage fans around folds, as well as “the bending and crowding of the cleavage surfaces, to accommodate themselves between the folds of the less yielding rock”, implying that “when we see a fold in a cleaved region, we can no more assert that it is of its original form” (p. 401).

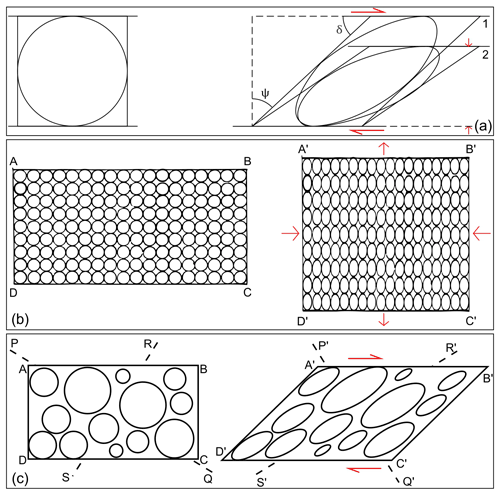
Figure 4 (a) Simple shear deformation according to Fisher (1884a, his Fig. 1). Deformed shape 1 corresponds to simple shear and 2 to simple shear plus contraction normal to the shear plane. Dashed lines and red arrows are added to the original figure to illustrate the shear angle ψ and its complementary δ. (b–c) Redrawn Figs. 1 to 3 of Van Hise (1896), showing pure shear (b) and simple shear (c) deformation of circular objects in a layer (ABCD). Cleavage will be parallel to lines $B^{\prime }{C}^{\prime }$ or $R^{\prime }{S}^{\prime }$, respectively. Red arrows are additions to the original figures.

Harker (1885a) discussed Fisher (1884a, b) first by stating that in simple shear, assuming no volume change and plane strain, a sphere of radius r=b would turn into an ellipsoid of radii $a>b>c$, and ac=b². However, the strain ellipsoids calculated from deformed fossils (e.g., from Haughton, 1856) indicate that a and b are often similar, whereas c is relatively very small, “thus giving an ellipsoid very like a flat oblate spheroid” (Harker, 1885a, p. 16), implying a decrease in volume proportional to the ratio $ac/b^{\mathrm{2}}$ (assuming that b is unchanged, i.e., plane strain).

Harker (1885a) further argued against the shear-related deformation associated with cleavage formation in Fisher's theory, mostly because the amount of shear and the predicted cleavage orientations are “very different from anything recorded as occurring in nature” (p. 17). However, in giving his calculations, Harker did put forward the mathematical equations that describe the geometry of the strain ellipse in simple shear deformation! His first equation,

$$\begin{array}{}\text{(7)}& \cot \mathit{\delta }={\displaystyle \frac{a-c}{\sqrt{ac}}},\end{array}$$

relates the major and minor semiaxes of the strain ellipse (a>c), with the shear strain $\mathit{\gamma }=\tan \mathit{\psi }=\cot \mathit{\delta }$ (see Fig. 4a and Appendix A). The second equation relates the angle ϕ between cleavage (long axis of the ellipse) and the shear plane (θ^′ in modern notation), with the ratio between the principal axes of the ellipse (see Appendix A):

$$\begin{array}{}\text{(8)}& \tan \mathit{\varphi }=\sqrt{{\displaystyle \frac{c}{a}}}.\end{array}$$

In his reply, Fisher (1885) considered that the results of oblate ellipsoids obtained by Haughton (1856) were at least problematic, especially because of the assumption of a larger elongation in the cleavage–bedding intersection, which contrasts with much of the observed slates with stretching parallel to their cleavage dip. In explaining the progressive deformation during simple shear, Fisher remarked that the limbs of folds “would be alternately compressed and elongated”, depending on the changing orientation of bedding to the direction of shear:

If that were such that [bedding] made at first an acute angle with the direction of the shear [it] would be more and more crumpled as the shear went on, until such time as the axis of the folds became perpendicular to the direction of the shear. When that position had been passed, they would begin to be straightened out again (…) If, however, the bedding of the layers was at right angles, or at an obtuse angle, to the shear, they would never be crumpled at all but begin at once to be torn to pieces. Thus it appears that even the same amount of shear, which at one locality produces frilling [boudinage], may in another, not far off, produce schistosity: the difference of effect depending upon different inclinations between the layers and the shear at the two places. (Fisher, 1885, pp. 175–176)

This explanation indicates an outstanding understanding of the kinematics of simple shear deformation, which would explain, for example, folded boudins and boudinaged folds (cf. Ramsay and Huber, 1983).

8 A refinement of Sorby's progressive deformation model

Almost simultaneously with discussing Fisher's ideas, Harker published a remarkable model for development of cleavage during progressive deformation of a sedimentary rock (Harker, 1885b). He started pointing out that the difference between simple shear and flattening was the volume loss related with the latter, which would result in an oblate strain ellipsoid, in opposition to the prolate ellipsoid resultant from constant-volume simple shear. Therefore, his aim was to evaluate whether the cleavage was formed by flattening (compression perpendicular to cleavage planes) or by shear (cf. Fisher, 1884b, 1885), and he simplified the problem to the question “whether the cleaved rocks have or have not suffered a total diminution of bulk” (Harker, 1885b, p. 266).

The model of Harker (1885b, pp. 266–267) starts with the lateral compression of a rock composed largely of long and flat fragments, without an original fabric. Compression would cause lateral shortening, “involving a corresponding decrease of bulk, and effected by the closer packing of the constituent fragments, accompanied by the expulsion of the greater part of the interstitial water”. Packing would tend to arrange the fragments in a position normal to the compression, forming an initial cleavage and resulting in a strain ellipsoid of the form $a\approx b>c$, i.e., an oblate strain ellipsoid comparable to the one described by Haughton (1856), for which Harker gives the first genetic interpretation.

After the packing reaches a limit, volume loss by this process is hampered; thus “continued pressure would give rise to a vertical expansion of the mass compensating the horizontal compression” (Harker, 1885b, p. 267). The deformation in this stage is of constant volume, with an increase of the long axis of the ellipsoid and a proportional decrease of the short axis ($a>b>c$), and the cleavage is best developed due to the more perfect arrangement of the long and flat particles perpendicular to the compression (cf. Sorby, 1853).

A further stage of continued shortening would result in the involvement of mineralogical and chemical processes, with the formation of a coarser foliation due to metamorphism and without constant volume. The related ellipsoid would turn out as an “excessively elongated and flattened” one (a≫c). This model as put forward by Harker (1885b), like the model mentioned above by Sorby (1880), is remarkably still valid today, as a description of the progressive strain in sedimentary rocks (see Ramsay and Huber, 1983, pp. 185–188, fig. 10.24).

In relation to the relative timing of folding and cleavage, examples of which were provided by Fisher (1884b), where it seemed that cleavage always postdated folding, Harker (1885b) considered that they were two distinct modes of satisfying compression. He also considered the following:

Contortion of the strata should precede cleavage is a matter of no surprise, if the latter involve an actual condensation of bulk while the former is a mere change of position. In accordance with this we frequently find contortion without cleavage, but cleavage without contortion never. (p. 267)

He also related microfolds with “a first step towards a cleavage structure”, making reference to the Ausweichungsclivage of Heim (1878) and the close-joints cleavage between crenulation folds of Sorby (1880, Fig. 3d).

9 State of the art during the late 19th century

Harker's study of rock strain and cleavage crystallized in his report to the British Association for the Advancement of Science (Harker, 1886, read in 1885). This paper was an up-to-date compilation of facts and theories concerning strain, but I will highlight here the original contributions that arise from Harker's own careful observations and mathematical deductions. At first, he gives some “order of thoughts” to several parameters dispersed throughout the previous literature, such as the concept of ratio of volume change of the strain ellipsoid (volumetric stretch in modern textbooks), which is $abc/r^{\mathrm{3}}$ (deformed volume over volume of the undeformed sphere of radius r). In plane strain, b=r; thus the ratio is defined by $ac/b^{\mathrm{2}}$. For oblate ellipsoids where a=b, the ratio is $c/b$.

In more depth, Harker explains mathematically the simple shear deformation, complementing the foregoing discussion of Fishers' papers. His equations for the axes of the strain ellipsoid are

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{s+\sqrt{s^{\mathrm{2}}+\mathrm{4}}}{\mathrm{2}}}:\mathrm{1}:{\displaystyle \frac{\sqrt{s^{\mathrm{2}}+\mathrm{4}}-s}{\mathrm{2}}},\end{array}$$

where s is the shear strain (γ in modern notation) and equals the tangent of the shear angle (ψ) (cf. with Eqs. (3)–(67) of Ramsay, 1967; see Appendix A). Harker states a firm argument against the theory of Phillips (1844), Laugel (1855), and Fisher (1884a), which ascribes the planes of cleavage as planes of shear, since that theory implies “(i) no compression of the rock in a direction perpendicular to the cleavage planes and (ii) no distortion of plane objects lying in planes parallel to the cleavage” (Harker, 1886, p. 819), both opposite to observed facts. Harker considers that simple shear can be regarded (and is simpler to do so) “as a compression perpendicular to the cleavage planes accompanied by a compensating expansion along the cleavage dip (…) with the necessary rotation concurrent with it” (pp. 819–820). This would give an ellipsoid different from the one obtained by Sorby (1856) (with volume loss) and Haughton (1856) (oblate, a≈b). Harker's argument was completely that of a strain-dependent fabric, i.e., independently of the mechanism and the presence or lack of volume loss, the cleavage as a resultant fabric of deformation would be parallel to the larger diameter of the strain ellipsoid or the XY plane in modern notation. This would apply even to constrictional strain ellipsoids ($a\gg b\approx c$), which cause “the fibrous structure which Professor A. Heim denominates linear cleavage as distinguished from ordinary plane cleavage” (Harker, 1886, p. 820).

Another important observation in Harker's work is the fact of the underestimation of the bulk strain of a rock determined from the measurement of strain in fossils (or other imbedded objects). “A hard substance imbedded in a softer matrix would evidently yield but slightly, or not at all, to any compression to which the mass as a whole might be subjected”, as is effectively observed in rocks where some “fossils of more solid substance or stouter form are comparatively unchanged in shape, while those of slighter build exhibit a marked deformation” (p. 525).

Harker (1886) discussed with much clearness Haughton's equations and methodology (Haughton, 1856) and added two equations that widen their applicability. First, when the undeformed shape of the fossil is unknown, but one finds in the same bedding plane two deformed fossils in orthogonal positions, the first with length (m) perpendicular to a_H, the second with breadth (n) in that position (e.g., fossils 1 and 2, respectively, of Fig. 2b), it is possible to obtain $\mathit{\rho }/a_{\mathrm{H}}$:

$$\begin{array}{}\text{(10)}& {\left({\displaystyle \frac{\mathit{\rho }}{a_{\mathrm{H}}}}\right)}^{\mathrm{2}}={\displaystyle \frac{m_{\mathrm{1}}}{n_{\mathrm{1}}}}{\displaystyle \frac{n_{\mathrm{2}}}{m_{\mathrm{2}}}}.\end{array}$$

The second equation allows us to obtain $\mathit{\rho }/a_{\mathrm{H}}$ when the undeformed shape is unknown, and one deformed fossil lies in the bedding plane with length and breadth oblique to dip and strike, α and β being the angles that length and breadth make with the bedding dip line, respectively (fossil 3 in Fig. 2b):

$$\begin{array}{}\text{(11)}& {\left({\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}\right)}^{\mathrm{2}}=\tan \mathit{\alpha }\tan \mathit{\beta }.\end{array}$$

Harker also discussed in depth the different cleavage refraction relationships, summarizing the concepts put forward by several researchers before him but paying special attention to the explanation of this phenomenon in terms of strain. He demonstrated mathematically the conclusions of Sorby (1853), obtaining the general equation of the strain ellipse in the ac plane (XZ plane) for the less competent and more competent lithologies (e.g., shale and sandstone in Sorby's example), which are ellipses rotated angles ϕ and ϕ^′ from the bedding plane, respectively (Fig. 5). The equation for the shale's strain ellipse is (Harker, 1886)

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{{\left(x\cos \mathit{\varphi }+y\sin \mathit{\varphi }\right)}^{\mathrm{2}}}{a^{\mathrm{2}}}}+{\displaystyle \frac{{\left(y\cos \mathit{\varphi }-x\sin \mathit{\varphi }\right)}^{\mathrm{2}}}{c^{\mathrm{2}}}}=\mathrm{1},\end{array}$$

where x and y are the Cartesian axes parallel and perpendicular to bedding, respectively. If a and c are the semiaxes of the strain ellipse for the shale and $a^{\prime },c^{\prime }$ the corresponding semiaxes for the sandstone, then the ratio between the volumetric stretches of both lithologies is $\mathit{\mu }=ac/a^{\prime }{c}^{\prime }$. According to Sorby (1853), the change in volumetric stretch across the lithologic boundary is only possible in a direction normal to bedding, therefore parallel to the y axis (Fig. 5). Thus the equation for the strain ellipse in the sandstone can be conveniently written (Harker, 1886)

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{{\left(x\cos \mathit{\varphi }+\mathit{\mu }y\sin \mathit{\varphi }\right)}^{\mathrm{2}}}{a^{\mathrm{2}}}}+{\displaystyle \frac{{\left(\mathit{\mu }y\cos \mathit{\varphi }-x\sin \mathit{\varphi }\right)}^{\mathrm{2}}}{c^{\mathrm{2}}}}=\mathrm{1}.\end{array}$$

For any ellipse centered at the origin and inclined to the coordinate axes an angle α, with the general equation $A{x}^{\mathrm{2}}+Bxy+C{y}^{\mathrm{2}}=\mathrm{1}$, we know that tan $\mathrm{2}\mathit{\alpha }=B/\left(AC\right)$. Therefore, we can relate angles ϕ and ϕ^′ using this relationship and Eq. (13), from which we obtain coefficients A, B, and C:

$$\begin{array}{}\text{(14)}& {\displaystyle }\cot \mathrm{2}{\mathit{\varphi }}^{\prime }={\displaystyle \frac{\left(\frac{{\cos }^{\mathrm{2}}\mathit{\varphi }}{a^{\mathrm{2}}}+\frac{{\sin }^{\mathrm{2}}\mathit{\varphi }}{c^{\mathrm{2}}}\right)-\left(\frac{{\sin }^{\mathrm{2}}\mathit{\varphi }}{a^{\mathrm{2}}}+\frac{{\cos }^{\mathrm{2}}\mathit{\varphi }}{c^{\mathrm{2}}}\right)}{\mathrm{2}\mathit{\mu }\sin \mathit{\varphi }\cos \mathit{\varphi }\left(\frac{\mathrm{1}}{a^{\mathrm{2}}}-\frac{\mathrm{1}}{c^{\mathrm{2}}}\right)}}\text{(15)}& {\displaystyle }\cot \mathrm{2}{\mathit{\varphi }}^{\prime }={\displaystyle \frac{\cot \mathit{\varphi }\left({\mathit{\mu }}^{\mathrm{2}}{a}^{\mathrm{2}}-c^{\mathrm{2}}\right)-\tan \mathit{\varphi }\left(a^{\mathrm{2}}-{\mathit{\mu }}^{\mathrm{2}}{c}^{\mathrm{2}}\right)}{\mathrm{2}\mathit{\mu }\left(a^{\mathrm{2}}-c^{\mathrm{2}}\right)}}.\end{array}$$

This equation, developed by Harker (1886), demonstrates that except when cleavage is normal or parallel to bedding, ϕ^′ will be always larger than ϕ. This is because μ<1 when the volume loss of the shale is larger than that of the sandstone, as observed.

Harker (1886) also noticed that the equation for the strain ellipse of the sandstone is also useful to explain the thickness increase in the fold hinges of contorted beds within a shaly matrix. Using Eq. (13) (see Appendix A), he gave the following equation that relates the semiaxes of the sandstone strain ellipse ($a^{\prime },c^{\prime }$) with the angle ϕ:

$$\begin{array}{}\text{(16)}& {a^{\prime }}^{\mathrm{2}}+{c^{\prime }}^{\mathrm{2}}={\displaystyle \frac{\begin{array}{c}\left(\mathrm{1}+{\mathit{\mu }}^{\mathrm{2}}\right)\left(a^{\mathrm{2}}+c^{\mathrm{2}}\right)-\left(\mathrm{1}-{\mathit{\mu }}^{\mathrm{2}}\right)\\ \left(a^{\mathrm{2}}-c^{\mathrm{2}}\right)\cos \mathrm{2}\mathit{\varphi }\end{array}}{\mathrm{2}{\mathit{\mu }}^{\mathrm{2}}}}.\end{array}$$

From this equation and the relationship $ac/\mathit{\mu }=a^{\prime }{c}^{\prime }$, it is possible to obtain the axial ratio $a^{\prime }/c^{\prime }$ of the strain ellipse for the sandstone and evaluate its variations with the position of a fold. When ϕ is 90^∘, i.e., in the positions of the fold where bedding and cleavage are perpendicular (hinges), this ratio is largest, or the stretch parallel to the axial surface is a maximum. With smaller values of ϕ in the fold limbs, the ratio decreases.

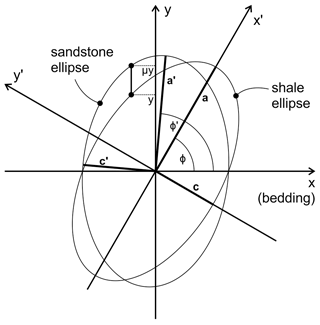
Figure 5 Geometry of the strain ellipses of the sandstone and shale layers of Fig. 1, which are rotated ellipses with reference to the Cartesian x, y coordinates. μ is the ratio between the volumetric stretches of both lithologies.

In an extensive discussion regarding the close-joints cleavage of Sorby (1858, 1880), and its likeness with the Ausweichungsclivage of Heim (1878), Harker (1886) concluded that this spaced cleavage structure could not be regarded as true joints which form due to extension of the rock. However, he considered them faults, i.e., associated with shearing at a microscopic scale during lateral compression. This may be considered an incorrect interpretation by modern structural geologists, but see Bell and Hobbs (2010).

10 Refinement of concepts and differences between pure and simple shear

Nearly at the same time, Charles Richard Van Hise, with the aid of the mathematician Leander Miller Hoskins, deepened the discussion of rock strain and cleavage formation. Van Hise (1896) considered that the parallel alignment of old and new particles, either flattened (cf. Sharpe, 1947) and/or rotated (cf. Sorby, 1853), was the main cause of the cleavage, the latter understood as the property of some rocks to part in a preferred orientation. Even if Van Hise highlighted the difference between pure shear (pure shortening as he called it) and simple shear, he supported the premise, as Harker (1885, 1886) did, that the cleavage planes in both deformation types would form parallel to the largest diameter of the strain ellipsoid (Fig. 4b–c). In the case of simple shear, though, he clarified the following:

The cleavage is at right angles to the direction of greatest shortening of the area in its final position (…) This resultant position is not normal to the final direction of greatest pressure, but at any given moment the deformation occurring is itself normal to the pressure (…) Thus the cleavage develops strictly in the normal planes, but its position by the rotation of simple shearing is inclined to the final direction of pressure. (Van Hise, 1896, p. 457, italics are mine)

This seems aimed to explain, in a still rudimentary manner, the difference between instantaneous and finite strain and its relation to stress.

Another researcher, George Ferdinand Becker, discussed the applicability of his theories on the characteristics of homogeneous strain (Becker, 1893) to the development of rock fabrics, especially cleavage (Becker, 1896, 1904). He argued, following Phillips (1844), that “cleavage is due to weakening of cohesion along planes of maximum tangential strain”, and consequently “a belt of slate is equivalent to a great fault distributed over an infinite number of infinitesimal steps” (Becker, 1904, pp. 11–12). The theoretical outcome of this has already been discussed when asserting Harker's contributions, but it is worth mentioning that Becker (1904) developed analogue models designed to test his ideas against what he called “Sharpe's theory” (cleavage perpendicular to the smallest axis of the strain ellipsoid). He made a series of experiments subjecting pieces of wax, ceresin, and clay to either uniaxial compression (simulating experiments made by Tyndall in 1856) or to simple shear using a “scission engine”. In all cases, after the experiment he indurated the deformed cake by cooling the ceresin or baking the clay, and afterward he hammered the cake to separate it in the supposed cleavage planes. The planes of separation, which are actually shear fracture planes, are obviously oblique to the applied compression in all cases. In his own words: “In no case have I broken a cake which behaved as it should on Sharpe's theory” (Becker, 1904, p. 19). This is most evident for the experiments with simple shear, since Becker clearly considered that the cleavage formed parallel to the shear plane or planes of constant area, which he also attributed to planes of maximum shear strain. This latter assumption is not in general justified (Hobbs et al., 1976; see Ramsay and Huber, 1983, Appendix D), and it is clear that Becker's cleavage in his simple shear models is actually a set of shear fractures (Becker, 1904, Figs. 24–27).

Later, Charles Kenneth Leith in 1905 published a very good memoir where he kept the distinction, originally recognized by Sorby (1853, 1880) and later by Heim (1878), between what we know today as continuous and spaced cleavage (see above). Leith proposed the genetic terms “flow cleavage” for the first, which is “the cleavage developing during rock flowage (or the deformation of rock without conspicuous fracture)”, and “fracture cleavage” for the latter, a cleavage “developing through the deformation of rock by fracture and subsequent cementation” (Leith, 1905, p. 19). This latter term has had relative success of usage, persisting for almost a century. In a more descriptive note, Leith highlighted that flow cleavage included structures that exist due to the parallel arrangement of the mineral constituents, while fracture cleavage groups structures that do not depend on that arrangement. His explanation for fracture cleavage was that it “occurs through the development of incipient fractures or the welding or cementation of parallel fractures, yielding parallel planes of weakness” (p. 66).

In his paper, Leith made a great contribution to the study of ductile deformation leading to flow cleavage, especially noticing many microstructures characteristic of mylonitic deformation, as we know them today. He described a number of structures that showed the relationship between the cleavage and the directions of shortening and elongation in the rock (pp. 102–106), concluding the following:

Wherever the directions of shortening and elongation of a rock mass can be determined with certainty, any flow cleavage which may be present is normal to the total [finite] greatest shortening which the rock has undergone. (p. 106)

Leith (1905) followed the lineaments stated by Van Hise (1896) regarding the relationship between pure shear (irrotational strain), simple shear (rotational strain), and development of flow cleavage:

During irrotational strain, flow cleavage tends to develop uniformly in the plane normal to the greatest principal stress [or instantaneous strain] (…) During rotational strain flow cleavage tends to develop at any instant in planes or lines normal to the greatest stress (…) in which elongation is occurring at that instant (…) but rotation constantly carries it from this position. Just as the total elongation of the rock mass in rotational strain is the net result of all the strains developed at successive stages of deformation, so cleavage, (…) is the net result of all the strains, and its average position may be finally inclined somewhat to the greatest principal stress. (Leith, 1905, pp. 112–113)

This reflects a deep understanding of the relationship between strain and structure and defines this type of cleavage as a non-material foliation according to modern terminology (see Twiss and Moores, 2007, pp. 399–400). In this manner it also laid the difference with the parallel arrangement of original particles due to rotation as material planes or lines during deformation, which in simple shear will rotate towards the shear plane at different velocities than the non-material foliation (the finite strain axes), although “whether the deformation is by rotational or irrotational strain a sufficient amount of it may bring about substantial parallelism of all particles, new or old” (Leith, 1905, pp. 114–115).

11 “Fracture” versus pressure–solution cleavage

Fracture cleavage is of special interest here, since it connects with the last part of this paper. This type of cleavage, as mentioned, includes basically two kinds of structures that in modern terminology are crenulation cleavage and disjunctive cleavage (Powell, 1979). Both kinds are characterized by a domainal structure, in Leith's words an “intermitted character, by which is meant its confinement to certain definite planes separated by considerable thicknesses of rock which show no tendency to cleave” (Leith, 1905, p. 120), in modern terms cleavage domains and microlithons. The cleavage domains are what Leith called “incipient parallel fractures or actual fractures which by subsequent welding or cementation remain planes of weakness” (pp. 119–120). His Fig. 34 (from Dale, 1896) illustrating “fracture cleavage in slate emphasized by ferruginous staining” is an excellent example of a smooth disjunctive cleavage. Since the cleavage domains were considered as minute faults or shear fractures, it is obvious that the interpretation that follows is that fracture cleavage must be “inclined to the elongation of the rock mass” (Leith, 1905, p. 121).

Two months prior to passing away, Sorby's last paper was read before the Geological Society of London (Sorby, 1908). It is not surprising that the dissertation was related in part to the study of rock strain and less surprising that on his last work Sorby pointed in the direction in which future research would assist to a highly improved understanding of penetrative rock structures related to strain. In the part of this paper of more interest to us, he described the microscopic structure of the so-called “slip surfaces” related to his close-joints cleavage, or fracture cleavage in the terminology of Leith (1905):

As seen under the microscope, these slip surfaces in section look like very thin black lines, on the whole perpendicular to the line of pressure, as shown by small contortions of the bedding; yet they are seldom straight, being, as it were, drawn by a shaking hand. They are sometimes parallel for a short distance but usually unite with or branch into each other. (Sorby, 1908, pp. 222–223)

Sorby also described the differential development of these surfaces in lithologies of varying hardness, always describing them as microfaults.

However, in the same paper he further discussed the process of pressure–solution (coining this name) that he had described decades before (Sorby, 1863b, 1865). A description of a “tooth-like structure”, stylolites in modern terminology, as “layers of dark, apparently bituminous, material extending over a considerable area, passing up and down like larger and smaller interlocking teeth”, inclined him to the interpretation that “the most probable origin of the bitumen is that it is a residue of the solution of the limestone and that solution of carbonate of lime has occurred is clearly proved (…) it seems as though both pressure and solution have acted” (Sorby, 1908, p. 225). The relationship between these surfaces of pressure–solution and the development of cleavage in calcareous slates was manifest, as well as the occurrence of pressure–solution perpendicular to the overburden during diagenesis, although Sorby recognized that the cause of these structures was one “about which we know little or nothing” (p. 226).

12 Concluding remarks

High-quality research on rock strain is carried out regularly in current times. Modern technologies, such as electron microscopy or isotope geochronology, among others, allow geoscientists to constrain variables that were unimaginable more than a century ago. Many of the recent advances in strain studies are anchored in theoretical concepts and definitions established around the mid-20th century, which have been encompassed in seminal structural geology textbooks and scientific papers. In turn, most of these concepts have been taken from landmark discoveries made during the 19th century. However, the lack of citation of these older papers in recent years suggests that many modern researchers are unaware of them.

As an example, consider Eqs. (2) and (6) from Haughton (1856), which constitute the basic equation relating length changes and strain and the first equations used to obtain strain from distorted fossils. These were commented on in Ramsay's books (Ramsay, 1967; Ramsay and Huber, 1983) and remained the mathematical basis of some strain quantification techniques (cf. Breddin, 1955), but Haughton's contribution is rarely mentioned in modern papers. Equation (1) from Sorby (1853) constitutes another interesting example. This simple equation relating changes of angles with an imposed strain is at the basis of many methods of deformation analysis (Wettstein, 1886; Ramsay, 1967), and Sorby should be given the merit of obtaining this equation by means of observation, experimentation, and the ability of putting into a simple algebraic expression the logical explanation of his results. Similarly, we may emphasize that during 1884–1885, discussion of contrasting ideas between Fisher and Harker resulted in the mathematical descriptions of simple shear deformation (Eqs. 7–9), and further analysis by Van Hise and Leith developed a profound understanding of the differences between pure and simple shear deformation.

In order to bring attention to these landmark works from the 19th century, I reviewed here the research that gave origin to the foundations of rock strain investigations, especially regarding deformation fabrics such as cleavage. These basic concepts include the relationship between shortening directions with cleavage formation, elemental equations leading to strain quantification, constant-volume versus volume-loss deformation, the strain ellipsoid concept, line rotation during progressive strain, simple versus pure shear strain geometries, or pressure–solution deformation mechanisms. I focused also on some of the more prominent mathematical conclusions made during that span, which I developed in depth in the Appendix with the aim that their significance is widely acknowledged. All these concepts were born in a span of 73 years, obtained by the simple model of scientific methodology: intelligent observation, precise measurements, and the proposal of logical ways to explain the data. I hope to have succeeded in showing the high standards of observation and mathematical analysis that led to these landmarks more than 100 years ago.

Appendix A

The following section is intended to give a detailed explanation of where the equations mentioned in the text come from, in some cases using concepts that are commonplace in modern structural geology texts. Unfortunately this kind of detail lacks in most technical papers, but I believe that this is of detriment to the understanding of the mathematical background of many fundamental concepts on rock strain.

Consider a Cartesian coordinate system with a circle of radius r centered at the origin, which deforms into an ellipse of semiaxes $a=r\sqrt{{\mathit{\lambda }}_{\mathrm{1}}}$ and $c=r\sqrt{{\mathit{\lambda }}_{\mathrm{2}}}$, where $\sqrt{{\mathit{\lambda }}_{\mathrm{1}}}\sqrt{{\mathit{\lambda }}_{\mathrm{2}}}$ are the principal stretches of the given deformation, with $\sqrt{{\mathit{\lambda }}_{\mathrm{1}}}/\sqrt{{\mathit{\lambda }}_{\mathrm{2}}}=R$. Line $\stackrel{\mathrm{‾}}{OP}$ makes an angle φ with the x coordinate axis, and this line transforms after deformation in line $\stackrel{\mathrm{‾}}{Op}$ at an angle φ^′ with the same axis (Fig. A1). Equation (1) establishes the relationship of the tangent of angle φ with the tangent of angle φ^′. In the example of Fig. A1 it is clear that the length from the x axis to point P is tan φr. This distance becomes $\tan \mathit{\phi }r\sqrt{{\mathit{\lambda }}_{\mathrm{2}}}$ after deformation, which is the length from the x axis to point p. Therefore, this allows us to conveniently write

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}& \tan {\mathit{\phi }}^{\prime }={\displaystyle \frac{\tan \mathit{\phi }r\sqrt{{\mathit{\lambda }}_{\mathrm{2}}}}{r\sqrt{{\mathit{\lambda }}_{\mathrm{1}}}}}\\ & \tan {\mathit{\phi }}^{\prime }=\tan \mathit{\phi }{\displaystyle \frac{\sqrt{{\mathit{\lambda }}_{\mathrm{2}}}}{\sqrt{{\mathit{\lambda }}_{\mathrm{1}}}}}=\tan \mathit{\phi }{R}^{-\mathrm{1}},\end{array}\end{array}$$

which gives the relationship of the angles $\mathit{\phi },{\mathit{\phi }}^{\prime }$ with the axial ratio $R=a/c$.

Equation (2) is obtained from the general equation of an ellipse aligned with the coordinate axes and centered at the origin, such as illustrated in Fig. A2. From that figure, we know that

$$\begin{array}{}\text{(A2)}& {\displaystyle }{x}_{\mathrm{1}}=\cos \mathit{\varphi }\mathit{\rho }\text{(A3)}& {\displaystyle }{y}_{\mathrm{1}}=\sin \mathit{\varphi }\mathit{\rho }.\end{array}$$

Therefore, we replace x and y for x₁ and y₁ in the equation of the ellipse:

$$\begin{array}{}\text{(A4)}& \mathrm{1}={\displaystyle \frac{{\cos }^{\mathrm{2}}\mathit{\varphi }}{b_{\mathrm{H}}^{\mathrm{2}}}}{\mathit{\rho }}^{\mathrm{2}}+{\displaystyle \frac{{\sin }^{\mathrm{2}}\mathit{\varphi }}{c_{\mathrm{H}}^{\mathrm{2}}}}{\mathit{\rho }}^{\mathrm{2}}\end{array}$$

and obtain the form of Eq. (2):

$$\begin{array}{}\text{(A5)}& {\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}^{\mathrm{2}}}}={\displaystyle \frac{{\cos }^{\mathrm{2}}\mathit{\varphi }}{b_{\mathrm{H}}^{\mathrm{2}}}}+{\displaystyle \frac{{\sin }^{\mathrm{2}}\mathit{\varphi }}{c_{\mathrm{H}}^{\mathrm{2}}}},\end{array}$$

from which Eq. (3) is obtained. We want to find $a_{\mathrm{H}}/b_{\mathrm{H}}$ and $a_{\mathrm{H}}/c_{\mathrm{H}}$ using Eq. (3) for a pair of planes of angles ϕ, ϕ^′ and known distortions $a_{\mathrm{H}}/\mathit{\rho }$ and $a_{\mathrm{H}}/{\mathit{\rho }}^{\prime }$:

$$\begin{array}{}\text{(A6)}& {\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}}{{\mathit{\rho }}^{\mathrm{2}}}}={\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\varphi }}{b_{\mathrm{H}}^{\mathrm{2}}}}+{\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\varphi }}{c_{\mathrm{H}}^{\mathrm{2}}}}\text{(A7)}& {\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}}{{{\mathit{\rho }}^{\prime }}^{\mathrm{2}}}}={\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}{\cos }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }}{b_{\mathrm{H}}^{\mathrm{2}}}}+{\displaystyle \frac{a_{\mathrm{H}}^{\mathrm{2}}{\sin }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }}{c_{\mathrm{H}}^{\mathrm{2}}}}.\end{array}$$

We can simplify $a_{\mathrm{H}}^{\mathrm{2}}$ because it has no effect in our problem and convert these expressions into two linear equations with two unknowns, where $\mathrm{1}/b_{\mathrm{H}}^{\mathrm{2}}=x$, $\mathrm{1}/c_{\mathrm{H}}^{\mathrm{2}}=y$, and $\mathrm{1}/{\mathit{\rho }}^{\mathrm{2}}=c_{\mathrm{1}}$, $\mathrm{1}/{{\mathit{\rho }}^{\prime }}^{\mathrm{2}}=c_{\mathrm{2}}$.

$$\begin{array}{}\text{(A8)}& {\displaystyle }{c}_{\mathrm{1}}={\cos }^{\mathrm{2}}\mathit{\varphi }x+{\sin }^{\mathrm{2}}\mathit{\varphi }y\text{(A9)}& {\displaystyle }{c}_{\mathrm{2}}={\cos }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }x+{\sin }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }y.\end{array}$$

Figure A1 Relationship between orientations of lines before and after deformation.

Figure A2 Geometry of an ellipse like the one in Fig. 2c, in the Cartesian coordinate system.

Using Cramer's rule,

$$\begin{array}{}\text{(A10)}& {\displaystyle }x={\displaystyle \frac{c_{\mathrm{1}}{\sin }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }-c_{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\varphi }}{{\cos }^{\mathrm{2}}\mathit{\varphi }{\sin }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }-{\sin }^{\mathrm{2}}\mathit{\varphi }{\cos }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }}}\text{(A11)}& {\displaystyle }y={\displaystyle \frac{c_{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\varphi }-c_{\mathrm{1}}{\cos }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }}{{\cos }^{\mathrm{2}}\mathit{\varphi }{\sin }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }-{\sin }^{\mathrm{2}}\mathit{\varphi }{\cos }^{\mathrm{2}}{\mathit{\varphi }}^{\prime }}}.\end{array}$$

Replacing $\mathrm{1}/{\mathit{\rho }}^{\mathrm{2}}=c_{\mathrm{1}}$, $\mathrm{1}/{{\mathit{\rho }}^{\prime }}^{\mathrm{2}}=c_{\mathrm{2}}$, multiplying $(-\mathrm{1}/-\mathrm{1})$ in both equations, and solving the differences of the squares in the numerators and the denominators gives

$$\begin{array}{}\text{(A12)}& {\displaystyle }x={\displaystyle \frac{\left(\frac{\sin \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}+\frac{\sin {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}\right)\left(\frac{\sin \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}-\frac{\sin {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}\right)}{\begin{array}{c}\left(\cos \mathit{\varphi }\sin {\mathit{\varphi }}^{\prime }+\sin \mathit{\varphi }\cos {\mathit{\varphi }}^{\prime }\right)\\ \left(\sin \mathit{\varphi }\cos \mathit{\varphi }{}^{\prime }-\cos \mathit{\varphi }\sin {\mathit{\varphi }}^{\prime }\right)\end{array}}}\text{(A13)}& {\displaystyle }y={\displaystyle \frac{\left(\frac{\cos {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}+\frac{\cos \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}\right)\left(\frac{\cos {\mathit{\varphi }}^{\prime }}{\mathit{\rho }}-\frac{\cos \mathit{\varphi }}{{\mathit{\rho }}^{\prime }}\right)}{\begin{array}{c}\left(\cos \mathit{\varphi }\sin {\mathit{\varphi }}^{\prime }+\sin \mathit{\varphi }\cos {\mathit{\varphi }}^{\prime }\right)\\ \left(\sin \mathit{\varphi }\cos \mathit{\varphi }{}^{\prime }-\cos \mathit{\varphi }\sin {\mathit{\varphi }}^{\prime }\right)\end{array}}}.\end{array}$$

Replacing $\mathrm{1}/b_{\mathrm{H}}^{\mathrm{2}}=x$, $\mathrm{1}/c_{\mathrm{H}}^{\mathrm{2}}=y$, multiplying both sides of the equations for $a_{\mathrm{H}}^{\mathrm{2}}$, and using the identity $\sin (x\pm y)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$ in the denominators, we obtain the forms of Eqs. (4) and (5).

Harker (1885) used interesting geometric principles to obtain a useful relationship between the shear strain and the maximum and minimum semiaxes of the strain ellipse in simple shear (i.e., plane strain, equal area deformation). This is given in Eq. (7), which can be derived from the following example. Consider a circle of radius r inscribed in a square, which after simple shear becomes an ellipse of semiaxes a>c inscribed in a parallelogram, such as in Fig. A3.

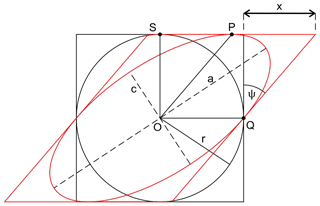
Figure A3 Deformation of a circle inscribed in a square into an ellipse inscribed in a parallelogram (red).

We know that $\stackrel{\mathrm{‾}}{OQ}=\stackrel{\mathrm{‾}}{OS}=r$ and that the uppermost point on the circle was displaced to the right by a distance $x=\stackrel{\mathrm{‾}}{SP}$. We also know that the area of the circle equals that of the ellipse; thus

$$\begin{array}{}\text{(A14)}& \begin{array}{rl}& \mathit{\pi }{r}^{\mathrm{2}}=\mathit{\pi }ac\\ & r=\sqrt{ac}.\end{array}\end{array}$$

Consider triangle OSP, from which we obtain that

$$\begin{array}{}\text{(A15)}& \begin{array}{rl}& {\stackrel{\mathrm{‾}}{OS}}^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{SP}}^{\mathrm{2}}={\stackrel{\mathrm{‾}}{OP}}^{\mathrm{2}}\\ & {\mathrm{r}}^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{SP}}^{\mathrm{2}}={\stackrel{\mathrm{‾}}{OP}}^{\mathrm{2}}.\end{array}\end{array}$$

Since $\stackrel{\mathrm{‾}}{OP}$ and $\stackrel{\mathrm{‾}}{OQ}$ are conjugate diameters of the ellipse, we know from the second theorem of Apollonius that they have the following property:

$${\stackrel{\mathrm{‾}}{OQ}}^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{OP}}^{\mathrm{2}}=a^{\mathrm{2}}+c^{\mathrm{2}}.$$

Replacing from Eqs. (A14) and (A15),

$$\begin{array}{}\text{(A16)}& \begin{array}{rl}& r^{\mathrm{2}}+\left(r^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{SP}}^{\mathrm{2}}\right)=a^{\mathrm{2}}+c^{\mathrm{2}}\\ & ac+ac+x^{\mathrm{2}}=a^{\mathrm{2}}+c^{\mathrm{2}}\\ & x^{\mathrm{2}}=a^{\mathrm{2}}+c^{\mathrm{2}}-\mathrm{2}ac\\ & x=a-c.\end{array}\end{array}$$

Finally, Eq. (7) from Harker (1885) gives the shear strain $\mathit{\gamma }=\tan \mathit{\psi }=\cot \mathit{\delta }$ as $x/r$, which from Eqs. (A14) and (A16) is

$$\begin{array}{}\text{(A17)}& \mathit{\gamma }={\displaystyle \frac{a-c}{\sqrt{ac}}}.\end{array}$$

To obtain Eq. (8) from Harker (1885), consider the following system of equations that are solved by the coordinates (x,y) of point Q when the coordinate axes coincide with the principal axes of the ellipse (Fig. A4):

$$\begin{array}{}\text{(A18)}& \left\{\begin{array}{l}{x}^{\mathrm{2}}+y^{\mathrm{2}}=ac\\ \frac{x^{\mathrm{2}}}{c^{\mathrm{2}}}+\frac{y^{\mathrm{2}}}{c^{\mathrm{2}}}=\mathrm{1}.\end{array}\right.\end{array}$$

The first one is the equation of the circle of radius $r=\sqrt{ac}$ (Eq. A14) and the second one the equation of the ellipse centered at the origin with semiaxis a parallel to coordinate axis x. Both contain point Q.

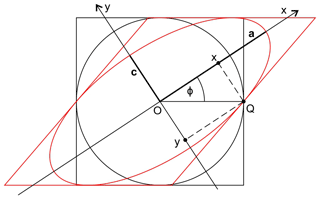
Figure A4 Geometry of the ellipse from Fig. A3, and its angle ϕ with the shear plane, considering Cartesian coordinates parallel to semiaxes ac.

The solutions of x²,y² that satisfy this system are

$$\begin{array}{}\text{(A19)}& {\displaystyle }{x}^{\mathrm{2}}={\displaystyle \frac{a^{\mathrm{2}}c}{(a+c)}}\text{(A20)}& {\displaystyle }{y}^{\mathrm{2}}={\displaystyle \frac{a{c}^{\mathrm{2}}}{(a+c)}}.\end{array}$$

Consider now the angle of interest, ϕ, which is the slope of the ellipse with respect to the shear plane parallel to $\stackrel{\mathrm{‾}}{OQ}$. We know that $\tan \mathit{\varphi }=y/x$, and from Eqs. (A19) and (A20), we can obtain the following relationship:

$$\begin{array}{}\text{(A21)}& \begin{array}{rl}& {\displaystyle \frac{y^{\mathrm{2}}}{x^{\mathrm{2}}}}={\displaystyle \frac{\frac{a{c}^{\mathrm{2}}}{(a+c)}}{\frac{a^{\mathrm{2}}c}{(a+c)}}}={\displaystyle \frac{c}{a}}\\ & {\displaystyle \frac{y}{x}}=\sqrt{{\displaystyle \frac{c}{a}}}=\tan \mathit{\varphi },\end{array}\end{array}$$

which is Eq. (8) from Harker (1885).

The expressions used by Harker (1886) for the semiaxes a and c of the strain ellipsoid in Eq. (9) are comparable to Eq. (3-67) of Ramsay (1967), since from Eq. (9),

$$\begin{array}{}\text{(A22)}& {\displaystyle }\begin{array}{rl}& a\text{or}c={\displaystyle \frac{\pm s+\sqrt{s^{\mathrm{2}}+\mathrm{4}}}{\mathrm{2}}}\\ & {\left(a\text{or}c\right)}^{\mathrm{2}}={\left({\displaystyle \frac{\pm s+\sqrt{s^{\mathrm{2}}+\mathrm{4}}}{\mathrm{2}}}\right)}^{\mathrm{2}}\\ & a^{\mathrm{2}}={\displaystyle \frac{s^{\mathrm{2}}+\mathrm{2}+s\sqrt{s^{\mathrm{2}}+\mathrm{4}}}{\mathrm{2}}}\end{array}\text{(A23)}& {\displaystyle }{c}^{\mathrm{2}}={\displaystyle \frac{s^{\mathrm{2}}+\mathrm{2}-s\sqrt{s^{\mathrm{2}}+\mathrm{4}}}{\mathrm{2}}}.\end{array}$$

These are equivalent to the mentioned equation from Ramsay (1967), where γ is used instead of s, and a², c² are the quadratic extensions λ₁,λ₂.

Equation (10) allows us to obtain the distortion in a plane when two symmetric fossil forms of the same kind are found with length and breadth conveniently oriented (Fig. 2b, fossils 1 and 2). From Eq. (6) it follows that for fossil 1, with length m₁ parallel to ρ and breadth n₁ parallel to a_H,

$$\begin{array}{}\text{(A24)}& {\displaystyle \frac{\mathit{\rho }}{a_{\mathrm{H}}}}{\displaystyle \frac{M}{N}}={\displaystyle \frac{m_{\mathrm{1}}}{n_{\mathrm{1}}}},\end{array}$$

where M and N are the unknown length and breadth of the undeformed fossil. For fossil 2, in a position perpendicular to the former,

$$\begin{array}{}\text{(A25)}& {\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}{\displaystyle \frac{M}{N}}={\displaystyle \frac{m_{\mathrm{2}}}{n_{\mathrm{2}}}}.\end{array}$$

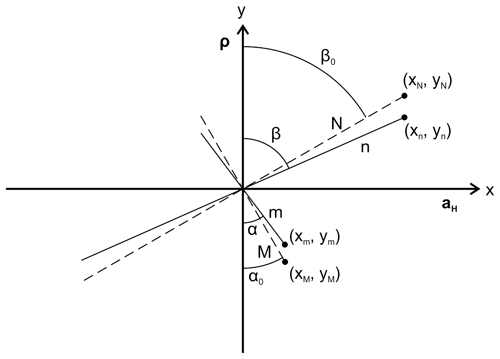
Figure A5 Relationship between angles of length m and breadth n of fossil 3 in Fig. 2b and their undeformed counterparts M and N.

Therefore, if we divide the deformed ratios $m/n$ of the two forms, as in Eq. (10), we obtain

$$\begin{array}{}\text{(A26)}& \left({\displaystyle \frac{\mathit{\rho }}{a_{\mathrm{H}}}}{\displaystyle \frac{M}{N}}\right)/\left({\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}{\displaystyle \frac{M}{N}}\right)={\left({\displaystyle \frac{\mathit{\rho }}{a_{\mathrm{H}}}}\right)}^{\mathrm{2}}.\end{array}$$

If we found only one deformed fossil with length and breadth (m, n), forming angles α and β with the direction of ρ (fossil 3 of Fig. 2b), and unknown undeformed shape (M and N), then accounting for Eq. (6) we can express the ratios $a_{\mathrm{H}}/\mathit{\rho }$ as a function of the tangents of these angles in the deformed and undeformed state (Fig. A5):

$$\begin{array}{}\text{(A27)}& {\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}={\displaystyle \frac{x_m}{y_m}}{\displaystyle \frac{y_M}{x_M}}={\displaystyle \frac{\tan \mathit{\alpha }}{\tan {\mathit{\alpha }}_{\mathrm{0}}}}\text{(A28)}& {\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}={\displaystyle \frac{x_n}{y_n}}{\displaystyle \frac{y_N}{x_N}}={\displaystyle \frac{\tan \mathit{\beta }}{\tan {\mathit{\beta }}_{\mathrm{0}}}}.\end{array}$$

From these equations, it follows that

$$\begin{array}{}\text{(A29)}& {\displaystyle }\tan \mathit{\alpha }={\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}\tan {\mathit{\alpha }}_{\mathrm{0}}\text{(A30)}& {\displaystyle }\tan \mathit{\beta }={\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}\tan {\mathit{\beta }}_{\mathrm{0}}.\end{array}$$

Since ${\mathit{\alpha }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{0}}=\mathrm{90}{}^{\circ }$, then tan α₀tan β₀=1; therefore

$$\begin{array}{}\text{(A31)}& \tan \mathit{\alpha }\tan \mathit{\beta }={\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}\tan {\mathit{\alpha }}_{\mathrm{0}}{\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}\tan {\mathit{\beta }}_{\mathrm{0}}={\left({\displaystyle \frac{a_{\mathrm{H}}}{\mathit{\rho }}}\right)}^{\mathrm{2}},\end{array}$$

which gives Eq. (11).

Equation (16) is obtained from considering the equation of the strain ellipse of the sandstone, as an ellipse of semiaxes $a{}^{\prime },c{}^{\prime }$, in a standard position (centered at the origin, aligned with the coordinate axes):

$$\begin{array}{}\text{(A32)}& {\displaystyle \frac{x^{\mathrm{2}}}{{a^{\prime }}^{\mathrm{2}}}}+{\displaystyle \frac{y^{\mathrm{2}}}{{c^{\prime }}^{\mathrm{2}}}}=\mathrm{1}.\end{array}$$

The matrix of the quadratic form associated with this equation is

$$\begin{array}{}\text{(A33)}& \left(\begin{array}{cc}\mathrm{1}/{a^{\prime }}^{\mathrm{2}}& \mathrm{0}\\ \mathrm{0}& \mathrm{1}/{c^{\prime }}^{\mathrm{2}}\end{array}\right).\end{array}$$

The trace of this matrix is $\mathrm{1}/{a^{\prime }}^{\mathrm{2}}+\mathrm{1}/{c^{\prime }}^{\mathrm{2}}$ (the sum of the coefficients of x² and y²), which is invariant with respect to a rotation of the axes. We can consider that the rotated ellipse represented by Eq. (13) is obtained after a rotation of the standard ellipse of Eq. (A26). The matrix of the quadratic form associated with the equation of a rotated ellipse centered at the origin is

$$\begin{array}{}\text{(A34)}& \left(\begin{array}{cc}A& B/\mathrm{2}\\ B/\mathrm{2}& C\end{array}\right),\end{array}$$

and the trace of this matrix is A+C. Therefore, since the trace of both matrices is the same, it follows that

$$\begin{array}{}\text{(A35)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{1}}{{a^{\prime }}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{1}}{{c^{\prime }}^{\mathrm{2}}}}& =\left({\displaystyle \frac{{\cos }^{\mathrm{2}}\mathit{\varphi }}{a^{\mathrm{2}}}}+{\displaystyle \frac{{\sin }^{\mathrm{2}}\mathit{\varphi }}{c^{\mathrm{2}}}}\right)\\ & +\left({\displaystyle \frac{{\mathit{\mu }}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\varphi }}{a^{\mathrm{2}}}}+{\displaystyle \frac{{\mathit{\mu }}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\varphi }}{c^{\mathrm{2}}}}\right)\end{array}\text{(A36)}& {\displaystyle \frac{\mathrm{1}}{{a^{\prime }}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{1}}{{c^{\prime }}^{\mathrm{2}}}}={\displaystyle \frac{{\cos }^{\mathrm{2}}\mathit{\varphi }+{\mathit{\mu }}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\varphi }}{a^{\mathrm{2}}}}+{\displaystyle \frac{{\sin }^{\mathrm{2}}\mathit{\varphi }+{\mathit{\mu }}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\varphi }}{c^{\mathrm{2}}}},\end{array}$$

where in Eq. (A35) we replaced the values of A and C from Eq. (13) (see Eq. 14). Using the identities ${\sin }^{\mathrm{2}}\mathit{\varphi }=\left(\mathrm{1}-\cos \mathrm{2}\mathit{\varphi }\right)/\mathrm{2}$ and ${\cos }^{\mathrm{2}}\mathit{\varphi }=\left(\mathrm{1}+\cos \mathrm{2}\mathit{\varphi }\right)/\mathrm{2}$, and remembering that $ac=a^{\prime }{c}^{\prime }\mathit{\mu }$, Eq. (A36) can be rearranged into Eq. (16).