The configuration of the Pontus Euxinus in Ptolemy's Geography

This article aims to explain how Ptolemy could have constructed a map of the Pontus Euxinus (Black Sea), as described in his Geography, under the assumption that his sources were similar to those that have come down to us. The method employed is based on the comparison of Ptolemy's data with corresponding information from other ancient sources, revealing the most conspicuous similarities and differences between them. Three types of information are considered as possible “constituent elements” of Ptolemy's map: latitudes, coastline lengths, and straight-line distances. It is argued that the latitudes Ptolemy used for the key points determining the overall shape of the Pontus (Byzantium, Trapezus, the mouth of the Borysthenes and the Cimmerian Bosporus, the mouth of the Tanais, etc.) were most likely inherited from earlier geographers (Eratosthenes, Hipparchus, and Marinus). In exactly the same way, Ptolemy's data on the circumference of the Pontus and the length of the coastal stretches between the key points (from the Thracian Bosporus to Cape Karambis, Sinope, Trapezus, and the mouth of the Phasis, etc.) closely correlate with the corresponding estimates reported by other geographers (Eratosthenes, Artemidorus, Strabo, Pliny, Arrian, and Pseudo-Arrian), which implies that Ptolemy drew on similar coastline length information. The shortening of Ptolemy's west coast of the Pontus (from the Thracian Bosporus to the mouth of the Borysthenes) relative to the corresponding distances reported by other sources is explained by his underestimation of the circumference of the Earth. The lengthening of Ptolemy's north-east Pontus coast (from the Cimmerian Bosporus to the mouth of the Phasis) can, in part, be accounted for by his attempt to incorporate the straight-line distances across the open sea reported by Pliny. Overall, Ptolemy's configuration of the Black Sea can be satisfactorily explained as a result of fitting contradictory pieces of information together that were inherited from earlier geographical traditions.

1 Introduction

The Geographical Guide (more commonly known as simply the Geography) by Claudius Ptolemy is a unique document containing a description of the earliest known, relatively detailed, and realistic map of the “Old World” (ca. 150 CE). This work is rightly regarded as the culmination of the entire tradition of ancient geographical science (Aujac, 2015; see Berggren and Jones, 2000, for a general introduction). On the one hand, in terms of its content, the Geography encompasses knowledge accumulated during the preceding centuries: it lists over 6300 place names – more than any other ancient geographical treatise. On the other hand, in terms of its form, it was a revolutionary breakthrough that paved the way for the European cartography of the Age of Discoveries. The innovativeness of the Geography was determined by the task Ptolemy set himself, namely, to devise a handy, yet mathematically rigorous and easily reproducible method of making a map of the world. To that end, he began to specify the positions of all geographical localities in the form of latitude and longitude coordinates, as had already been accepted in the astronomy of the time for recording the positions of celestial bodies (Defaux, 2017, pp. 45, 47, 54; Graßhoff et al., 2017, p. 484). Thus, the core of Ptolemy's Geography (six of eight books) consists of a catalogue of toponyms and their coordinates. In essence, his work became the first “digital map” in history (for a similar assessment, see Isaksen, 2011, p. 260). In this sense, all medieval copies of Ptolemy's maps were essentially derivatives of the text from his Geography, just as all modern reconstructions of his map are. Therefore, “Ptolemy's map” and his “Geography” are terms that can be used interchangeably as synonyms: Ptolemy's map is just another way to refer to the substance of his Geography. That was Ptolemy's major innovation and the fundamental difference between his work and those of earlier geographers, who only provided coordinates for the most important points.

Despite its universal recognition and extraordinary role in history, Ptolemy's Geography remains one of the least understood geographical works of the past. This is largely due to the fact that until recently there was neither a reliable edition of the Geography nor a recognized methodology for analysing this kind of source. Everything began to change with the new edition from Stückelberger and Graßhoff (2006), which not only provided a complete and verified text of the Geography for the first time but also included an electronic database of all localities mentioned in it and their Ptolemaic coordinates. With this edition, Ptolemy's Geography has become a veritable bonanza of knowledge for researchers from different fields and a testing ground for competing approaches and hypotheses (for a similar assessment, see Defaux, 2017, pp. 11–12).

The fundamental challenge the Geography poses to researchers is its opaqueness: Ptolemy gives us almost no clues to his sources or working methods (Isaksen, 2013, p. 47; Defaux, 2017, pp. 12, 163, 255; Graßhoff et al., 2017, pp. 484, 488; for more details see Sect. 3). No matter how diverse and numerous his sources may have been, all of them were completely remoulded into a uniform gazetteer of localities with their coordinates. Consequently, almost nothing is known about the initial data and how they were processed by Ptolemy to obtain coordinates for each locality. Therefore, the Geography has a better chance of being understood when studied, so to speak, as a kind of physical object: via the analysis of its internal structure and comparison with other similar objects. There are only two basic types of such objects: other ancient geographical sources and modern maps.

Recent studies devoted to the Geography, as different as they are, largely share a common methodological stance: they attempt to analyse Ptolemy's data via comparison with the modern map and, in particular, to reconstruct his sources and methods through the distortions he made (see e.g. Livieratos et al., 2008; Kleineberg et al., 2010; Mintz, 2011; Marx and Kleineberg, 2012; Rinner, 2013; Defaux, 2017; Abshire et al., 2016; Graßhoff et al., 2017). However, it would be methodologically more correct, before approaching Ptolemy from the viewpoint of modern knowledge, to consider his data in the context of his own time, i.e. via comparison with other ancient sources. Strangely enough, examples of this approach are still rather rare. They include the works of Gómez Fraile (2005), Urueña Alonso (2014), and Defaux (2017) on Ptolemy's Iberian Peninsula; Marx (2016) on the Atlantic coast of Africa; Arnaud (2017) on the coasts of the Mediterranean and the Red seas; and Rinner (2013) and Graßhoff et al. (2017) on Asia Minor.

The aim of the present paper is to continue this line of research by using the Pontus Euxinus (the Black Sea) as a test case. Ptolemy's description of the Pontus will be compared with corresponding information from other ancient sources to explain how the configuration of the Pontus that he describes (Figs. 1, 3, 4; also see Supplement 1, which described in the “Data availability” section of this paper) could have been constructed from these or similar sources which were presumably available to him (Supplement 2).

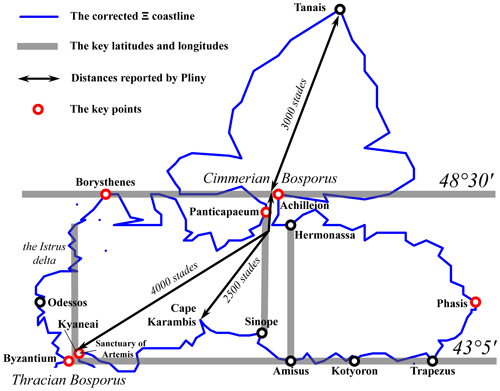
Figure 1 The “constituent elements” of the Pontus Euxinus in Ptolemy's Geography: the key points, latitudes, longitudes, and distances determining its basic outlines on his map (according to the corrected version of the Ξ recension). This and all of the following maps in the paper are drawn using the projection that Ptolemy ascribes to his immediate predecessor Marinus of Tyre (Geogr. 1.20.3–5). In modern terms, it is an equidistant cylindrical projection, in which the coordinate net consisted of two families of mutually orthogonal parallel lines, and distances are preserved along all the meridians and along only one parallel, which was the parallel of Rhodes (36^∘) in Marinus' case. Correspondingly, the east–west spacing of places situated north of this parallel is progressively expanded the further north they are.

2 Ptolemy's working method and sources

Understanding Ptolemy's Geography means reconstructing his working method and sources. Therefore, the question arises regarding what we know about them from Ptolemy's own words and our general understanding of ancient geography.

All of the characteristic properties of Ptolemy's Geography ultimately stem from its dual nature: in its form it appears as a uniform list of coordinates, but in its substance it remains a patchwork of different types of sources that present material in more traditional forms. Ideally, as Ptolemy states in Geography 1.4, all coordinates must be based on astronomical measurements of latitude and longitude. However, as such measurements were very few in practice, Ptolemy, as he himself points out, had to employ a two-step method of constructing a map (Defaux, 2017, pp. 166–169, 175; Graßhoff et al., 2017, pp. 486–488). First, a handful of points whose positions were considered as securely established (1.4.2) constituted the framework of the map. Ptolemy calls such points $\mathit{\theta }\mathit{\epsilon }\mathit{\mu }\stackrel{\mathrm{´}}{\mathit{\epsilon }}\mathit{\lambda }\mathit{\iota }o\mathit{\iota }$, i.e. the “foundations.” Second, all other points were located in relation to these “foundations” using other types of information (2.1.2). As the most common way known in antiquity to define geographical location was by using distance measurements, researchers unanimously agree that a good deal of Ptolemy's coordinates must have been based on distance data (Cuntz, 1923, p. 110; Knapp, 1996, pp. 30–35; Berggren and Jones, 2000, p. 26–27; Defaux, 2017, pp. 185, 318; Graßhoff et al., 2017, p. 507).

Next to nothing is known about the sources of Ptolemy's information, except for Marinus of Tyre (the first half of the second century CE), whom he himself presents as his immediate predecessor and the main source for his Geography¹. Therefore, the best we can do is to simply assume that Ptolemy and Marinus were able to use all types of information that was in principle available to a geographer of the second century CE and are now known to us from other surviving sources (for information on Ptolemy's sources, see e.g. Arnaud, 2017, pp. 92–98; Defaux, 2017, pp. 177–210; Graßhoff et al., 2017, pp. 492–493). Ptolemy's two-step method of map-making implies that two types of sources were of fundamental importance: (1) the works of the “mathematical” geographers who provided, among other thing, information on the latitudes and, in a very few cases, longitudes of the principal localities, and (2) the periploi and itineraries which described geographical space as a network of routes and distances in customary units (Greek stades, Roman miles, etc.) presented in the form “point A – distance – point B”. Evidently, the periploi shaped the coastal outlines of Ptolemy's map, whereas the itineraries determined the configuration of the internal regions (Knapp, 1996, pp. 32–35). As the outlines of Ptolemy's map are defined primarily by the coastlines, the role of the periploi must have been crucial. The only way to establish how and the extent to which Ptolemy used each type of source is to compare his data with surviving sources of the same type.

3 Method of analysis

The present study proceeds from the working hypothesis that Ptolemy's Geography was based on sources similar to those that have come down to us. Accordingly, the main tool for analysing Ptolemy's data is the comparison with other surviving sources to identify the most notable coincidences and discrepancies between them. Coincidences, when they are not likely to be accidental, can indicate the common origin of the data under comparison. Discrepancies, when they are fairly evident, demand an explanation and can be seen as signs of Ptolemy's manipulations of the source data. Of course, determining what may be considered accidental or evident inevitably involves a degree of arbitrariness and subjectivity. Therefore, only the clearest cases should be considered. For instance, the consensus is that, when Ptolemy's and Hipparchus' values for the latitudes of Byzantium (Istanbul) and the mouth of the Borysthenes (Dnieper) are essentially the same, it means that Ptolemy is following the tradition originating with Hipparchus here (see e.g. Berggren and Jones, 2000, p. 29; Defaux, 2017, pp. 192, 281; Graßhoff et al., 2017, pp. 494, 499; for more details, see Sect. 4). The same type of reasoning can apply equally well to coastline length data: when, for example, Ptolemy and Pseudo-Arrian use almost the same length of the coastline between key points such as the Thracian Bosporus (Bosporus Strait) and the mouth of the Phasis (Rioni), it is equally reasonable to conclude that they drew on the same sources (see Sect. 7.3).

Comparison and detection of close numerical correspondences with parallel sources allow us to deconstruct Ptolemy's map into separate “constituent elements” (see Heß, 2016 for information on the “Konstruktionselemente” of Ptolemy's map). Four types of data can be considered as possible material for such elements: latitudes and several longitudes of the key points, coastline length measurements, and straight-line distances across the open sea or inland. The patchwork nature of Ptolemy's Geography must have inevitably led to contradictions between different sources and to various distortions that ensured from his attempts to resolve these contradictions. A principal cause of distortions in Ptolemy's Geography was his adoption of an underestimated value for the circumference of the Earth (Shcheglov, 2016). This error had different impacts on the latitudinal and meridional outlines of his map. On the one hand, due to this error, all of the coastal outlines of the map, when expressed in terms of coordinates, are stretched in the east–west direction in comparison with the modern maps (Fig. 2). On the other hand, the coastal stretches that were oriented more or less in the north–south direction and enclosed between points with established latitudes must have been inevitably compressed by approximately the same proportion as the proportion by which Ptolemy's circumference of the Earth was underestimated. Thus, Ptolemy's latitude data were bound to come into conflict with the coastline length measurements recorded in other sources. The way Ptolemy sought to reconcile that conflict may provide us with important insight into his working methods.

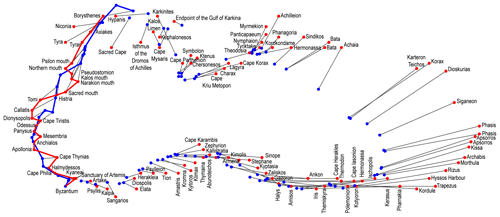
Figure 2 Displacement vectors connecting Ptolemy's coordinate points on the coasts of the Pontus (red) and their modern counterparts (blue), constructed using the Darcy 2.2 program (Vuidel, 2009). Byzantium is set as a reference point, so that it is the only error free location, against which all the displacements of Ptolemy's points relative to their counterparts on the modern map are measured. It is conspicuous that the outlines of Ptolemy's Pontus appear stretched in the east–west directions due to the underestimated value of the circumference of the Earth.

The analysis proceeds as follows. First, I demonstrate that the latitudes of several key points determining the basic latitudinal framework of the Pontus in Ptolemy's Geography can easily be traced back to earlier mathematical geographers (Sect. 4). Second, I compare Ptolemy's coastline length data with the corresponding values from other sources in order to identify the closest matches and the major differences between them (Sects. 6, 7). The closest matches can be considered the initial “constituent elements” of Ptolemy's map. Furthermore, I suggest a possible explanation for how Ptolemy could have reconciled the original measurements of the coastline length with the latitudes and longitudes of the key reference points and some other reports (Sects. 8, 9). In conclusion, I propose a working hypothesis regarding how Ptolemy's map of the Pontus could have been constructed from those “constituent elements” that have previously been identified.

4 Mathematical geographers as sources of the latitude data determining the outlines of the Pontus in Ptolemy's Geography

There are few ancient geographers that can be mentioned as Ptolemy's predecessors in the field of mathematical cartography: the aforementioned Marinus, Hipparchus (the third quarter of the second century BCE), and Eratosthenes (the third quarter of the third century BCE)². Those geographers established latitudes for only a handful of the most important localities. Among these localities, however, there were several key points which, as can easily be shown, determined the overall configuration of the Pontus on Ptolemy's map.

There was a cardinal difference between Ptolemy and his predecessors regarding the way they specified latitudes. Ptolemy's map was ideally conceived as what David Woodward called “equipollent-coordinate space”, in which “every place in the system is of equal geometric significance” (Woodward, 1990, pp. 119–120). Accordingly, every locality on Ptolemy's map must be ideally assigned its coordinates in degrees independently of all other localities. Earlier geographers used a system of special predetermined latitudes, each of which was keyed to one or several well-known localities. These latitudes were defined in terms of the duration of the longest day of the year and usually spaced at regular intervals of 1, 0.5 or 0.25 h (for example, 12.25, 12.5, 13 h, and so on)³. In the parlance of ancient mathematical geography, these latitudes were known mostly as κλíματα (sing. κλíμα). In a broader sense, the term κλíμα referred to the inclination of the celestial sphere to the plane of the horizon which characterized the latitude of the place. Therefore, it would not be a mistake to translate κλíμα as simply “latitude”. The concept of κλíμα (τα) was the most important tool available to pre-Ptolemaic geographers for constructing the framework of a mathematically rigorous map.

In the Geography, Ptolemy mentions a number of latitudes of this type. However, a more systematic exposition of essentially the same system of latitudes is found in his earlier work, the Almagest. There Ptolemy gives two tables of latitudes. One of these exposes the famous system of seven κλíματα (Almagest 2.12–13) or the main latitudes spaced at 1 h intervals starting from 13 h (Meroe in Ethiopia) to 16 h (the mouth of the Borysthenes). The other is the so-called “Shadow Table” (Almagest 2.6) which consists of 39 parallels from the Equator to the North Pole, including the seven κλíματα, although avoiding the term κλíμα. Five of these parallels relate to the Pontus and the Maeotis (Sea of Azov): those running through Massalia (Marseille; the longest day is 15.25 h, 43^∘4^′)⁴, the middle of the Pontus (15.5 h, 45^∘1^′), the mouth of the Borysthenes (16 h, 48^∘32^′), the middle of the Maeotis (16.25 h, 50^∘4^′), and the mouth of the Tanais (Don; 17 h, 54^∘1^′).

Many of the parallels from the Shadow Table are clearly seen on Ptolemy's map, forming its general outlines (Wurm, 1931, pp. 20–21, 30; Isaksen, 2013, p. 50, Fig. 3.4). Four relate to the Pontus and the Maeotis, whereas two are of cardinal importance in constituting the northern and southern sides of the Pontus (Fig. 1). The parallel of 15.25 h (43^∘5^′ in the Geography) determines the latitude of the whole southern coast, including the positions of Byzantium with the adjacent Thracian Bosporus, Amisus (Samsun), and Trapezus (Trabzon). The parallel of 16.5 h (48^∘30^′) determines the latitude of the northernmost points of the Pontus (the mouths of the Borysthenes; Hypanis, Southern Bug River; and Karkinites, the city of Tamyrake, which possibly refers to modern Dzharylhach), the southern coast of the Maeotis, and the Cimmerian Bosporus (the Kerch Strait and specifically Achilleion, on the Fontalovsky Peninsula, in both recensions of the Geography and Cape Myrmekion, Karantinny, only in Ω; for more details see Sect. 6.2 and Figs. 3–4). The parallel of 15.5 h (45^∘) marks the maximum east–west dimension of the Pontus (only in Ξ) between Odessus (Varna) in the west and the Phasis, which was well known in antiquity as the easternmost point of the Pontus. The parallel of 17 h (54^∘) marks the northernmost corner of the Maeotis with the mouth of the Tanais (Ptolemy's latitude for its western mouth is 54^∘10^′).

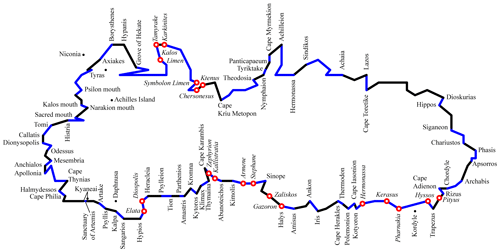
Figure 3 Ptolemy's coastline of the Pontus divided into 74 short stretches between the points that have counterparts in Pseudo-Arrian's Periplous. Points located in the wrong order are marked in red and displayed using italic text.

Figure 4 The outlines of the Pontus Euxinus according to the Ξ and Ω recensions of Ptolemy's Geography and a corrected version of the Ξ recension.

There are good reasons to suppose that the entire system of latitudes which formed the framework of Ptolemy's map was, by and large, inherited from Marinus of Tyre (Shcheglov, 2004, pp. 27–31). We at least know for certain that Marinus mentioned the parallel through the middle of the Pontus (Ptol. 1.16) and located Trapezus on the parallel through Byzantium (Ptol. 1.15.9).

Before Marinus, Ptolemy's Shadow Table and the system of seven κλíματα had earlier prototypes: Hipparchus' table of κλíματα and a set of parallels in Eratosthenes' geography, respectively. Hipparchus composed the earliest known table of κλíματα which constituted the most important part of his treatise Against the Geography of Eratosthenes (ca. 135–128 BCE) and was his main contribution to geographical science (Shcheglov, 2003–2007; Marx, 2015). As Hipparchus' treatise was lost, the only source of our knowledge regarding his table is a brief synopsis in Strabo's Geography (1.5.34–42 C131–135), which is our main source on ancient geography (ca. 23 CE)⁵.

The four aforementioned parallels discerned in the outlines of Ptolemy's Pontus are already found in Strabo's synopsis. The parallel of 15.25 h is said to pass through Massalia and Byzantium (F 51, 53, 54, 55, 59). The parallel of 15.5 h passed though “the regions of the Pontus about 1400 stades to the north of Byzantium,” which is essentially the same as Ptolemy's “the middle of the Pontus” (F 56)⁶. The parallel of 16 h crossed “the regions about the mouth of the Borysthenes” and the southern parts of the Maeotis (F 57)⁷. The parallel of 17 h passed through “the regions north of the Maeotis” (F 60) where the mouth of the Tanais was usually located (2.4.7 C107). Two of Ptolemy's seven κλíματα – that of the mouth of the Borysthenes and presumably that of the middle of the Pontus associated with the respective lengths of the longest day – can be traced further back to Eratosthenes' Geography (Roller, 2010, p. 64; Shcheglov, 2004, pp. 33–37).

In addition, it should be noted that several key points of Ptolemy's Pontus are clearly situated at the same longitudes: the mouths of the Istrus (Danube) lie approximately at the longitude of the Thracian Bosporus (56^∘15^′), the longitudes of Sinope (63^∘50^′; Sinop) and Panticapaeum (64^∘; Kerch) are almost the same, and Amisus and Hermonassa (Taman) lie on the meridian of 65^∘. These correspondences can hardly be coincidental and may also be viewed as elements of the framework underlying Ptolemy's map (Fig. 1).

5 Periploi as the sources of the coastline length data

The Pontus Euxinus was chosen as the subject of the present study because it provides especially rich material for comparing Ptolemy's data with other sources. The Pontus Euxinus is lucky, as its coastlines are described in the surviving sources in even more detail than the core regions of the Greco-Roman world. Of all the surviving periploi, only four give precise distances between all of the more or less notable points on the coast, and three of them are devoted to the Pontus: those composed by Menippus of Pergamon (the end of the first century BCE)⁸ and Flavius Arrian (the beginning of second century CE) served as the main sources for the third Periplous known as Pseudo-Arrian (the second half of the sixth century CE)⁹. As both Arrian's and Menippus' data were incorporated by Pseudo-Arrian's Periplous with only minor alterations and additions, it is reasonable to confine our investigation to the comparison between Ptolemy and Pseudo-Arrian. Interestingly, Pseudo-Arrian exhibits closer toponymic similarity to Ptolemy than Arrian¹⁰. Furthermore, as we will see in Sect. 7.2, there is also a striking similarity between Pseudo-Arrian and Ptolemy with respect to the distance data.

Pseudo-Arrian describes the perimeter of the Pontus as a succession of distances between 187 coastal points (53 in Europe and 134 in Asia) with the median length of 90 stades (see Supplement 2)¹¹. Ptolemy lists 142 points on the coast of the Pontus (57 in Europe and 85 in Asia; see Supplement 1), and at least 106 of them can be identified and localized on the modern map (Fig. 2; see Supplement 3)¹². Of this number, 90 points (37 in Europe and 53 in Asia) are shared by both sources (and 4 other points mentioned in the Periplous are placed far from the coast by Ptolemy and, thus, cannot be considered when determining its length)¹³. Excluding several points that Ptolemy places in the wrong order (Sect. 7.3), 74 coastal points are mentioned in both sources (29 in Europe and 45 in Asia) in the same geographical sequence (Fig. 3; see Supplement 4). All of these similarities make Pseudo-Arrian's Periplous the closest parallel to Ptolemy's description of the Pontus. Therefore, a comparison between them in Sects. 7–9 will constitute the core of our analysis.

A considerable amount of information about the coasts of the Pontus is contained in the Geography of Strabo (ca. 23 CE) and books III–VI of the Natural History of Pliny the Elder (ca. 79 CE)¹⁴, the two largest geographical compendiums that have come down to us from antiquity. Strabo describes a circumnavigation of the Pontus consisting of 33 segments, 27 of which have counterparts in Ptolemy's data (see Supplement 5)¹⁵. Strabo's chief source was most likely the Geographic Description of Artemidorus of Ephesus (ca. 104–100 BCE; for a general introduction, see Schiano, 2010). Pliny lists different estimates by earlier geographers of the entire perimeter of the Pontus¹⁶, of the respective lengths of its European and Asian sides (Table 1), and of the lengths of the coastal stretches between several principal points¹⁷. He also gives a rather detailed periplous of the Asian coast consisting of 14 segments ¹⁸.

Table 1 Length of the coastlines of the Pontus and the Maeotis according to Ptolemy and other ancient geographers (in stades). Ptolemy's data are given for both recensions (Ξ and Ω). The “Difference” columns show how much Ptolemy's data differ from the other geographers' estimates (expressed as a percentage of the latter). Some coastlines are measured differently on different lines, as marked by the indices attached to the distance values: “a” refers to values measured without the interval between Panticapaeum and Achilleion; “b” refers to values measured without the width of the Cimmerian Bosporus between Achilleion and Porthmion and the Porthmion–Myrmekion stretch; “c” refers to values measured from the Sanctuary of Zeus/Artemis to Panticapaeum; “d” refers to values measured from the Sanctuary of Zeus/Artemis to Myrmekion; and “e” refers to values measured from the Thracian Bosporus to Korokondame. On all other lines, the coastlines are measured without omissions.

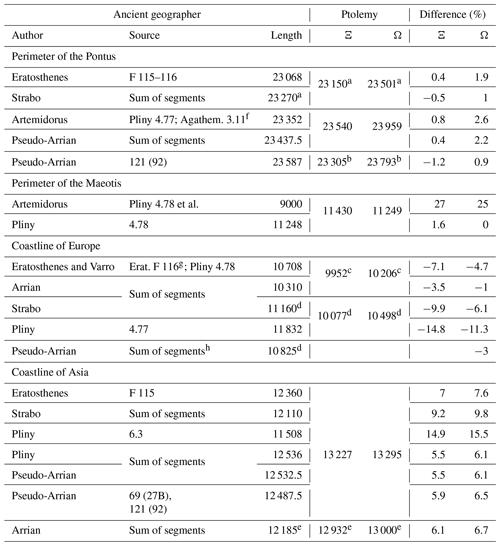
^f Agathemerus' text vaguely states that “the Pontus is 3350 stades”, although the dimension remains unclear (Diller, 1975, pp. 63, 69, 73). The most plausible explanation seems to be that the figure originally referred to the circumference of the Pontus, but its first numeral was lost. ^g Pliny seems to have mixed up Eratosthenes' figures for the European and the Asian coastlines, as indicated by the fact that the value of 1338.5 m.p. which he ascribes to the Asian coast at 6.3 is much lower than all the other estimates, but it almost coincides with the length of the European coast reported by Varro (Pliny 4.78: 1337.5 m.p.). ^h At 120 (91), Pseudo-Arrian estimates the distance from Porthmion to the Sanctuary of Zeus Ourios to be 11 100 stades, which is an obvious arithmetic mistake. For a possible explanation, see Diller (1952, pp. 104–105).

6 Difficulties to be taken into account

6.1 Determining the length of coastlines in Ptolemy's Geography

How can we compare Ptolemy's coastline length data, presented in the form of coordinates, with the information from other sources, expressed in terms of customary distance units? The correct solution would be to reconstruct how Ptolemy converted distances reported by his sources to the coordinates of his gazetteer and to reverse his method in order to extract the original distance data. Unfortunately, Ptolemy left us almost no clues as to his method. My contention is that it the most reasonable solution in this situation is follow the simplest and most natural approach, namely to take Ptolemy's Geography as what it essentially is, i.e. as a catalogue of spherical coordinates. A distance between two points on a sphere which are specified by the coordinates of latitude and longitude is an arc of the great circle that can be calculated using the rules of spherical trigonometry. Accordingly, I propose to calculate the length of Ptolemy's coastlines as the sum of individual arcs joining coastal points multiplied by the length of a degree of the great circle which he defines as 500 stades (Geogr. 1.7.1, 11.2). The distance between points A and B located on a sphere can be calculated using the formula $\cos S_{\mathrm{AB}}=\cos \mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{AB}}\times \sin$ (90^∘ − φ_A) × sin (90^∘ − φ_B) + cos (90^∘ − φ_A) × cos (90^∘ − φ_B), where S_AB is the distance between points A and B, Δλ_AB is the longitudinal interval between them, φ_A and φ_B are their latitudes, and all these values are expressed in degrees of the great circle¹⁹.

It should be emphasized that this approach is used only in the absence of better alternatives. It is hard to imagine that Ptolemy would have determined the coordinates of all the 6300 points listed in his Geography in the same way, performing complicated calculations for each of them. More likely, he would have calculated the coordinates for only a few reference points, and determined all the rest by means of simpler methods, for example, Pythagoras' theorem and/or simply a ruler and compass (Spaul, 1958; Defaux, 2017, pp. 255–257, 285–288, 306–308, 318–319; Graßhoff et al., 2017, pp. 498–499). Therefore, an alternative method for establishing the distances between Ptolemy's points would be to reverse this map-making procedure: first, plot their coordinates on a plane and then simply measure the distances with a ruler. However, a crucial obstacle to this approach is that we need to know what projection Ptolemy used when converting distances to coordinates, and this cannot be ascertained²⁰.

6.2 Two recensions of Ptolemy's Geography

The original of the Geography was lost and its text is reconstructed from the medieval manuscripts, the earliest of these date back to the end of the 13th century. The manuscripts are divided into two recensions, commonly denoted as Ξ and Ω, both dating back to antiquity. The Ξ recension is recognized as the earlier and more authentic, but it is represented by the sole manuscript “Vaticanus graecus 191” (available online at: http://digi.vatlib.it/view/MSS_Vat.gr.191, last access: 20 March 2020), which contains many errors, especially in numerals, and omits all of the coordinates for the eastern half of the map from Geogr. 5.13.16 onwards (for the whole of Asia except for Asia Minor, Sarmatia, and Armenia). The Ω recension includes many manuscripts, but, judging by many signs, it is secondary to Ξ (Burri, 2013, pp. 63–93, 540–542; Rinner, 2013, pp. 317, 322–323; Defaux, 2017, pp. 67–81, 127–162, 373–374, 412–414; Graßhoff et al., 2017, p. 507). Thus, both recensions should be considered, but in the case of significant discrepancies that cannot be explained by copying errors, the Ξ version should be preferred.

Both recensions contain scribal errors, which are not always easy to detect. The Ξ recension causes more difficulties: while Ω, which is a reconstruction based on the collation of many manuscripts, has been already cleaned of errors as much as possible, Ξ retains its original manuscript text without corrections. As Ξ is represented by only one manuscript, it is often difficult to determine whether there is an error or whether Ξ simply offers an alternative variant to Ω (for a similar assessment, see Defaux, 2017, p. 118). Nevertheless, several glaring inconsistencies in the Ξ version can be corrected in accordance with Ω (see Appendix A; Supplement 1; Fig. 4).

A general comment on the differences between Ξ and Ω is required. The perimeter of the Pontus totals 23 540 stades in Ξ and 23 959 in Ω. A similar excess of the Ω coastline length values over the corresponding Ξ values is observed in most cases, which is probably due to the fact that Ω, being the second recension, has a more detailed geometry of the coastlines than Ξ (Shcheglov, 2018a, p. 15). The difference of 419 stades between the Ξ and the Ω grand totals is rather significant, but it consists of 40 discrepancies between individual short stretches with the median mean value of 53 stades. As Ptolemy rounded all coordinate values to the nearest 1∕6^∘ in most cases, or even to 1∕4^∘, and 1^∘ equals 500 stades, his rounding margin was 41.7–62.5 stades in latitude and 27.6–45.7 stades in longitude (for latitudes between 43^∘ and 48.5^∘) on average. This means that, in almost half the cases, the differences between Ξ data and Ω data do not exceed the average rounding error allowed by Ptolemy. Simply put, both recensions can be viewed as slightly different interpretations of essentially the same distance data.

6.3 Uncertainties in identifying the end points and configuration of the coastlines

There are several difficulties regarding the starting and ending points of the coastlines. For instance, Pliny only vaguely describes both the European and the Asian coasts as stretching from “the mouth of the Pontus” (the Bosporus) to “the mouth of the Maeotis” (the Kerch Strait; Varro apud Pliny 4.78; Erat. F 116 = Pliny 5.47) or “from the Bosporus to the Maeotis Lake” (6.3) without indicating specific points. We can only assume that the geographers whose reports he transmits defined the end points of the coasts in nearly the same way as other sources that were fortunate enough to have survived. The limits of the Asian coastline are defined with no uncertainties: both Strabo (7.6.1 C319; 11.2.6 C494; 13.3.7 C543) and Pseudo-Arrian (67 [25B], 69 [27B], 119–121 [90–92]) measure it from the sanctuary of Zeus Ourios on the Bosporus, which corresponds to Ptolemy's sanctuary of Artemis (Moreno, 2007), to Achilleion at the narrowest point of the Kerch Strait. The start and end points of the European coastlines vary in different sources. As its start point, Pseudo-Arrian also takes the sanctuary of Zeus Ourios, which seems inconsistent as it is situated in Asia. Its end point is defined differently in different sources: Panticapaeum in Varro (Pliny 4.78), who possibly followed Eratosthenes (F 116 = Pliny 5.47); Myrmekion or Parthenion (supposedly located on Cape Fonar) in Strabo (11.2.6 C494); and Porthmion (supposedly located near Zhukovka) in Pseudo-Arrian. Meanwhile, Ptolemy locates Parthenion on the coast of the Maeotis, which is too far from its mouth (Fig. 3), and does not mention Porthmion at all²¹.

In order to minimize the influence of these uncertainties, I take Panticapaeum as the end point of the European coastline when comparing Ptolemy's data with the reports of Eratosthenes and Strabo, but in other cases, I use Myrmekion. It is also not clear, whether all of the geographers included the breadth of the straits in the perimeter of the Pontus. Pseudo-Arrian, Varro, and possibly Eratosthenes (if it was he whom Varro followed, see footnote g in Table 1) did not include the breadth of the Cimmerian Bosporus, and neither do I when comparing their reports with Ptolemy's data (Table 1).

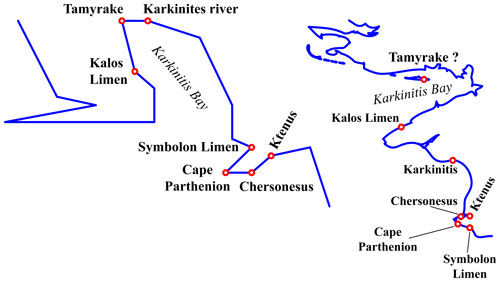
A similar difficulty concerns the fact that several points involved in the calculation of the coastline length according to Pseudo-Arrian are removed from the coastline and placed too far from it in Ptolemy (Figs. 2, 3): either inland (Kordyle in Cappadocia and Niconion in Moesia) or in the open sea (the island of Daphnousa near Bithynia and the Achilles island opposite to the mouth of the Borysthenes). Some other points are located in the wrong order by Ptolemy: Elata and Diospolis in Bithynia; Zephyrion and Kallistratia; Armene and Stephane; Zalyskos and Gazoron in Paphlagonia; and Hermonassa, Kerasuntos, Pharnakia, Hyssos, and Pityus in Cappadocia (Fig. 3; it was also noted by Rinner, 2013, p. 311). I have excluded all of these points from the calculations of the length of Ptolemy's coastline. Several points in the Crimea are displaced so intricately that it is impossible to decide which points are in error relative to one another (see Sect. 7.2; Fig. 9): Chersonesus, Ktenus (in the recess of the Sevastopol Bay), Symbolon Limen (Balaklava Bay), Karkinites (Yevpatoria), and Kalos Limen (Chernomorskoye).

In view of all these difficulties, all values of Ptolemy's coastline length used in the present paper can only be considered as approximate and be relied upon with every possible circumspection. Even a slight alteration of coordinates, a different choice of the coastline end points, or a different method of calculating its length would lead to somewhat different results. Therefore, when comparing Ptolemy's data with the distance data from other sources, only the clearest and most robust results should be considered.

7 Comparison of the coastline length data provided by Ptolemy's Geography, Pseudo-Arrian's Periplous, and other sources

Overall, information provided by ancient sources on the length of the Pontus coastlines can be divided into three groups: (1) the perimeter of the Pontus and the Maeotis (Table 1); (2) Pseudo-Arrian's data on the “short” coastal stretches between the neighbouring points that have counterparts in Ptolemy's Geography (Supplement 4); (3) the lengths of the “long” coastal stretches between the principal points (Table 2). The analysis below follows this scheme.

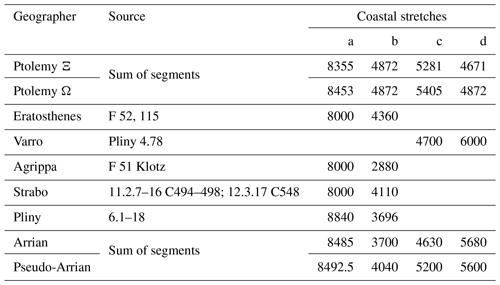
Table 2 Length of the four major coastal stretches of the Pontus according to Ptolemy and the other ancient geographers (in stades): “a” refers to the length from the Sanctuary of Artemis/Zeus Ourios to the Phasis; “b” refers to the length from the Phasis to Achilleion; “c” refers to the length from Panticapaeum to the Borysthenes; and “d” refers to the length from the Borysthenes to the Sanctuary of Artemis/Zeus Ourios.

7.1 The perimeter of the Pontus and the Maeotis

Table 1 shows that Ptolemy's value of the perimeter of the Pontus and those reported by the other authors coincide with remarkable accuracy. In all cases, the difference between them is less than 2 % of Ptolemy's value in the Ξ recension or less than 3 % of the Ω value. A similar coincidence is observed for the Maeotis: most sources repeat a rough estimate of its perimeter, 9000 stades, which was first recorded by Artemidorus (Agathemerus 3.10; Strab. 2.5.23 C126; 7.4.5 C310; Plin. 4.78; 6.207; Arrian, Periplous 30; Ps.-Arrian, 72 [43], 121 [92]). However, Pliny (4.78) gives a more precise value of 1406 m.p. or 11 248 stades which matches Ptolemy's data almost perfectly.

This result is just one instance of a more general observation made recently by Shcheglov (2018a) that the estimates of the coastline length of the major regions (such as the Iberian, Italian, and Arabian Peninsulas; the Adriatic and Caspian seas; the Persian Gulf; and so on.) reported by different ancient geographers almost always agree with the corresponding data in Ptolemy's Geography and with an accuracy of a few percent. This degree of agreement in itself can be used to argue that Ptolemy's map was probably built on the basis of coastline length data similar to those attested by the other sources.

7.2 The short coastal stretches in Ptolemy and Pseudo-Arrian

The comparison of Ptolemy's and Pseudo-Arrian's length values for the stretches between the 74 points mentioned in both sources presents a striking contrast to the results obtained in the previous subsection for the perimeter of the Pontus. Ptolemy's and Pseudo-Arrian's values for the short stretches always diverge so sharply that these differences cannot be reasonably accounted for in each individual case (Supplement 4 and Fig. 5).

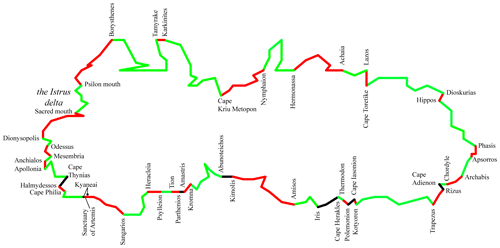
Figure 5 The segments of the Pontus coastline on Ptolemy's map that are stretched (green) or contracted (red) by more than 20 stades relative to the corresponding distances reported by Pseudo-Arrian.

This contradiction poses a crucial question with respect to understanding Ptolemy's method and the internal organization of his map: how can it be that the sharp disagreements between Ptolemy's and Pseudo-Arrian's data on the length of the short coastal stretches compensate for one another so precisely that as the length of the coastline under consideration (composed of a number of short stretches) increases, the difference between their estimates of its length decreases and, ultimately, almost vanishes?

The mechanism behind this transformation is in part elucidated when we analyse how the difference between Ptolemy's and Pseudo-Arrian's grand totals of the coastline length changes with the increasing number of individual short stretches of which the coastline is composed as a function of two factors: (1) the length of these short stretches (arranged in ascending order, disregarding their real geographic sequence) and (2) the real geographic sequence of these stretches. The results are illustrated in Figs. 6 and 8.

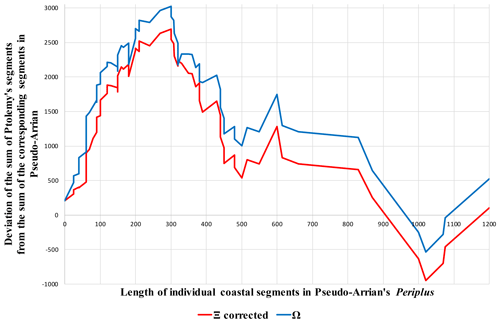
Figure 6 Deviation of the sum of the coastal segments in Ptolemy from the sum of the corresponding segments in Pseudo-Arrian's Periplous (y axis) as a function of Pseudo-Arrian's values for the length of individual segments (x axis).

Figure 6 shows how Ptolemy's grand total deviates from the corresponding values in the Periplous depending on the lengths of the individual stretches of which the grand total consists when they are arranged in ascending order. The graph clearly conforms to a Gaussian distribution: on the shortest stretches, Ptolemy's values for the total coastline length increasingly exceed those in the Periplous, and after a short “plateau” between 200 and 300 stades, Ptolemy's excess declines almost as steadily on the longer stretches until it reaches zero. To put it simply, Ptolemy tends to average the lengths of individual short stretches: to lengthen the shorter stretches and to shorten the longer stretches²². This result may be considered a manifestation of two basic properties of Ptolemy's space in the Geography, which can be conventionally denoted as “discreteness” and “horror vacui”. Both of these terms require clarification.

“Discrete” or “quantum” properties of Ptolemy's space manifest themselves in that there are only 12 possible values that the fractions of a degree contained in its coordinates can take on. All the values must be multiples of 5^′, but they strongly differ in how frequently they occur in Ptolemy's catalogue. The smaller the fraction, the rarer it is: the coordinates are expressed in integer degrees, without fractions, and those with a fraction of 1∕2^∘ are the most frequent; those with 1∕3 or 2∕3^∘ are less frequent; those with 1∕4 or 3∕4^∘ and 1∕6 or 5∕6^∘ are even less frequent; and those with 1∕12, 5∕12, 7∕12 and 11∕12^∘ are only used in a few exceptional cases. Most likely, this distribution of fractions resulted from Ptolemy's tendency to round all coordinate values as much as possible: in most cases, to the nearest 1∕6^∘, at least, i.e. within the margin of $\pm {\mathrm{5}}^{\prime }$ (for more details, see Marx, 2011).

The horror vacui refers to the general propensity of Ptolemy's map to smooth out the unevenness in the spatial distribution of points. The comparison with the modern coordinates reveals a clear pattern: the smaller the distance between the points in reality, the more it is overestimated by Ptolemy. To demonstrate this pattern, the following procedure can be used. Of the localities mentioned by Ptolemy on the coastlines of the Pontus, I selected 106 points which can be located on the modern map with sufficient confidence (Fig. 2 and Supplement 3). For each of these points, the average distance to its four nearest neighbours is calculated using both Ptolemy's and modern coordinates. Next, I found the ratio between the average distance values calculated from both Ptolemy's and the modern coordinates. Finally, Fig. 7 shows how this ratio varies depending on the average distances calculated from the modern coordinates when these are arranged in ascending order.

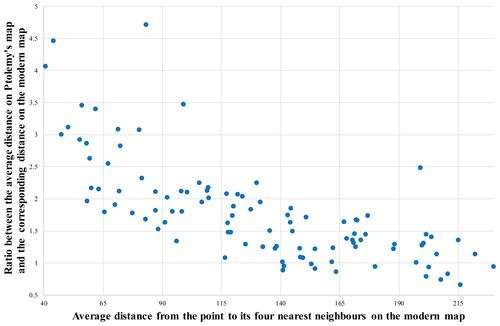
Figure 7 The overestimation of the average distances between neighbouring points on Ptolemy's map compared with the corresponding distances on the modern map as a function of the density of their distribution on the modern map. The x axis shows the average distance from each of the 106 points on the coasts of the Pontus to its four nearest neighbours, calculated using their modern coordinates. The y axis shows the ratio between the corresponding average distance value calculated using Ptolemy's coordinates and the average distance value indicated on the x axis.

Due to these two properties, Ptolemy's map had, figuratively speaking, a “low resolution”: it could reproduce the general outlines of large objects, but it was quite inaccurate with respect to small details and over short distances. Regarding the Pontus, Ptolemy grossly exaggerates the size of small but important features such as the Bosporus and the Kerch Straits, the Danube Delta, and the Dnieper-Bug estuary (Figs. 2, 5, 8)²³. Similarly, Ptolemy places the island of Daphnousa and the Achilles island too far from the coast and separates the river mouths and the harbours that were originally located next to each other by a considerable distance (Figs. 2–3): the harbour of Ancon at the mouth of the Iris (Pseudo-Arrian 28), Themiscyra at the mouth of the Thermodon (29), Apsorros and Phasis at the mouths of the rivers with the same names (40–41, 44–45 [3B]), Bata and the Bata Harbour (Strab. 11.2.14 C496), Sinda and the Sindicus Harbour (63 [21B]; cf. Strabo 11.2.14 C496), and Niconion near the mouth of the Tyras (90 [61]; cf. Strabo 7.3.16 C306).

7.3 The long coastal stretches in Ptolemy and Pseudo-Arrian

Figure 8 shows how the difference between Ptolemy's and Pseudo-Arrian's values of the coastline length varies geographically along the entire perimeter of the Pontus. It is clearly visible that Ptolemy alternates between progressively stretching and contracting the coastline relative to Pseudo-Arrian's data. The graph can be divided into four main parts which have distinctly different profiles and are delimited by the key points (see also Table 2): the Thracian Bosporus (more specifically, the starting point for both European and Asian coasts is the Sanctuary of Artemis/Zeus Ourios), the Cimmerian Bosporus (more specifically, Achilleion and Myrmekion on the Asian and European sides, respectively), the mouth of the Borysthenes (which marks the latitude of the northern limit of Ptolemy's Pontus), and the mouth of the Phasis (which was traditionally regarded as the easternmost point of the Pontus; see Dan, 2016, p. 248).

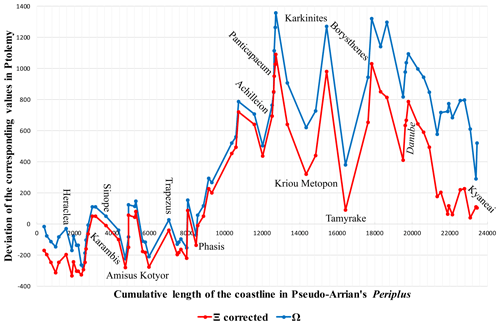
Figure 8 Difference between Ptolemy's and Pseudo-Arrian's coastline length data compared geographically. The x axis shows the cumulative sum of the coastal segments in Pseudo-Arrian, measured from the Sanctuary of Zeus anticlockwise around the Pontus. The y axis shows the deviation of Ptolemy's corresponding sum values from Pseudo-Arrian's sum values. Upward movement of the graph indicates that Ptolemy stretches the coastline relative to Pseudo-Arrian's data and vice versa.

Between the Thracian Bosporus and the Phasis, the difference graph oscillates around zero, so that the total length of this stretch in Ptolemy (8355 stades in Ξ and 8423 in Ω) is only 1.2 % or even 0.5 % less than the corresponding value given by Pseudo-Arrian (8462.5 stades in 121 [92]) or 2 % (in Ξ) and 1.2 % (in Ω) less than the sum of the individual short stretches listed by Pseudo-Arrian (8522.5), which slightly differs from his sum value. Remarkably, other geographers gave similar, although slightly lower, estimates for this stretch (see Table 2): Eratosthenes estimated 8000 stades (F 52 = Strabo 2.1.39 C91), which was accepted by Agrippa (F 51 Klotz, 1931, p. 448 = Pliny 6.3: from Chalcedon to the Phasis) and Strabo (12.3.17 C548), whereas Pliny estimated 8840 stades (6.1–18), and Arrian 8485 stades (the sum of individual segments; see Supplement 2).

The oscillation of the graph in Fig. 8 is evidently caused by the displacement of some points producing symmetric lengthening and shortening of the adjacent coastal stretches. Most remarkably, the key points remained almost unaffected by these displacements, as the graph showing the difference between Ptolemy's and Pseudo-Arrian's values most closely approaches zero at or near these points: Cape Karambis (Kerembe Burnu; the difference is −63 in Ξ and −5 in Ω), Sinope (−9 in Ξ and +50 in Ω), and Trapezus (−40 in Ξ and +28 in Ω).

Of course, we cannot be sure that, in each of these cases, Ptolemy drew on distances reported by Pseudo-Arrian or a similar source. However, the correspondences between their data are close and numerous enough to be regarded as instances of the same general pattern which suggests, at the very least, that Ptolemy considered distance data similar to those of Pseudo-Arrian. This result is, by and large, intuitively expected: what else could Ptolemy have relied on, if not his predecessors? What seems unexpected is how frequent and close the numerical coincidences between Ptolemy and Pseudo-Arrian are. Interestingly, no such coincidences are observed between Ptolemy and other sources (Strabo, Pliny, or Arrian). This allows us to consider the coincidences with Pseudo-Arrian as being those possible “constituent elements”, discussed in Sect. 3, of which Ptolemy's map was constructed.

Between the Cimmerian Bosporus and the Borysthenes, the oscillation of the graph resembles a saw because Ptolemy badly displaced several points on the Crimean Peninsula (Fig. 9). Chersonesus and Ktenus jumped to the east of Cape Parthenion (either Cape Fiolent or Cape Khersones), whereas Symbolon Limen shifted symmetrically to the west of it. Karkinites²⁴ and Kalos Limen moved out of the peninsula, so that Kalos Limen even found itself west of Tamyrake²⁵. Meanwhile, Pseudo-Arrian places Kalos Limen and Tamyraka at the east and west ends of the modern Karkinit Bay, respectively²⁶. However, what is more remarkable is that, even despite such errors and the extremely complex configuration of the coastline, the opposite distortions in Ptolemy's distance data compensate for one another almost completely, so that the total length of the coastline from Panticapaeum to the Borysthenes (5281 stades in Ξ and 5405 stades in Ω) matches Pseudo-Arrian's value (5200) with unexpected accuracy (Table 2).

Figure 9 The points of the western Crimea on Ptolemy's map and on the modern map.

The other two of Ptolemy's long coastal stretches, the Sanctuary of Zeus/Artemis–Borysthenes (4671 stades in Ξ and 4801 stades in Ω) and Phasis–Achilleion (4872 stades in both recensions), exhibit diametrically opposite distortions. The former is shorter by 960 (Ξ) or 799 (Ω) stades than the 5600 stades recorded in Pseudo-Arrian, whereas the latter is longer by 832 stades than the 4040 stades that is recorded in Pseudo-Arrian. Similar differences are seen between Ptolemy's data and the estimates reported by the other authors: the Bosporus–Borysthenes stretch measures 6000 stades according to Varro (Pliny 4.78), whereas the Phasis–Achilleion stretch is estimated at 4360 stades by Eratosthenes (F 52 = Strabo 2.1.39 C91; F 116 = Pliny 5.47), 4110 stades by Strabo (11.2.6–8, 14, 16 C494, 497–498; 12.3.17 C548), 3696 stades by Pliny (6.16–18), and even 2880 stades by Agrippa (F 51 = Pliny 6.3).

A similar pattern reveals itself from a comparison with Strabo's coastline length data: there is a drastic stretching of Ptolemy's coastline between the Sindica Harbour and the Cimmerian Bosporus, and a symmetrical contraction of the coastline between the Danube Delta and the Thracian Bosporus (Fig. 10).

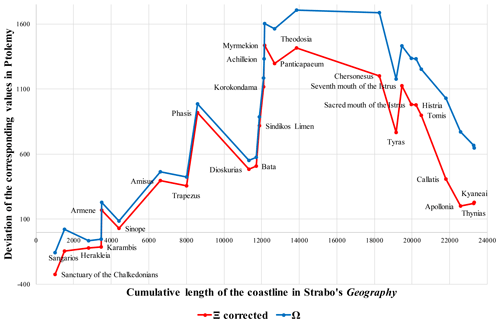
Figure 10 Difference between Ptolemy's and Strabo's coastline length data compared geographically. The x axis shows the cumulative sum of the coastal segments in Strabo, measured from the Sanctuary of Zeus anticlockwise around the Pontus. The y axis shows the deviation of Ptolemy's corresponding sum values from Strabo's sum values. Upward movement of the graph indicates that Ptolemy stretches the coastline relative to Strabo's data and vice versa.

These two major contradictions between Ptolemy's and Pseudo-Arrian's data require additional explanation (Sects. 8, 9).

8 Ptolemy's underestimation of the circumference of the Earth as a factor of the contraction of the Sanctuary of Artemis–Borysthenes coastal stretch

The Sanctuary–Borysthenes coastal stretch is clamped between the latitudes of Byzantium (43.083^∘) and the Borysthenes (48.5^∘; see Fig. 1), which go back to Hipparchus, at least, as was shown in Sect. 4. There are three remarkable coincidences regarding this coastline. First, the interval between the aforementioned Ptolemy's latitudes (48.5^∘–43.083^∘ = 5.416^∘) closely matches the corresponding actual value (5.49^∘)²⁷. Second, the length of the Sanctuary–Borysthenes coastal stretch according to Ptolemy, when expressed in angular terms as 7.8^∘, almost exactly coincides with the length of the line joining the corresponding points with the modern coordinates (7.82^∘; see Fig. 2 and Supplement 3)²⁸. Third, when expressed in stades, the length of this coastal stretch according to Ptolemy (4671 stades in Ξ and 4801 stades in Ω) is shorter than the corresponding estimates given by Pseudo-Arrian (5600) and Varro (6000) by approximately the same amount (17.1 % and 22.7 % in Ξ, respectively, or 14.3 % and 20 % in Ω, respectively), by which Ptolemy's value of the length of the Earth's meridian is below the true value, according to the most convincing interpretation (namely, by 16.7 % if 180 000 stades, or 33 300 km; for a more detailed discussion, see Shcheglov, 2016). Taken together, all of these coincidences suggest that the main factor responsible for the contraction of Ptolemy's Sanctuary–Borysthenes coastline was his adoption of this erroneous estimate.

9 The westward shift of the Cimmerian Bosporus (Kerch Strait) as a factor of the lengthening of the Phasis–Achilleion coastal stretch

The lengthening of Ptolemy's Phasis–Achilleion coastal stretch relative to Pseudo-Arrian's data counterbalances the shortening of the Sanctuary–Borysthenes stretch so precisely that it raises the suspicion that this is something more than a mere coincidence. This suspicion is increased by the fact that the same pattern of mutually cancelling lengthening and shortening of Ptolemy's coastlines is observed when comparing his data with the estimates of the length of the European and Asian coastlines of the Pontus given by the other authors (Eratosthenes, Strabo, and Pliny). In all cases, Ptolemy's coast of Europe turns out to be shorter by approximately 1000 stades, whereas the coast of Asia is proportionally longer (Tables 1, 2). Therefore, in this point, Ptolemy goes against the concerted opinion of all the other geographers.

While the shortening of Ptolemy's coast of Europe can be wholly explained by the contraction of the Sanctuary–Borysthenes coastline, the lengthening of the Asian side requires an additional explanation, unless one assumes that it was lengthened only to maintain the unchanged total perimeter of the Pontus. It remains especially unclear why, when comparing Ptolemy's data with Pseudo-Arrian's, the lengthening of the Asian side falls entirely on the Phasis–Achilleion stretch, rather than any other.

The lengthening of the Phasis–Achilleion stretch means, in other words, that Ptolemy placed the Cimmerian Bosporus further west than would be supposed by Pseudo-Arrian's distance data. A possible explanation for such a westward shift of the Bosporus can be found in a remarkable coincidence: the configuration of the Pontus in Ptolemy's Geography fits almost perfectly with the distances reported by Pliny: the straight-line distance between the two Bospori totals 4000 stades (4.77 from Polybius), the distance from Cape Karambis to the Cimmerian Bosporus is 2500 stades (2.245 from Artemidorus; see also Agathemerus 4.18, Diller, 1975, pp. 64, 70) and, further on, the straight-line distance from the mouth of the Maeotis to the mouth of the Tanais is 3000 stades (4.78; Fig. 1). It seems plausible, therefore, that the westward shift of the Bosporus, which led to the stretching of the Phasis–Achilleion coastline, was caused by Ptolemy's attempt to incorporate Pliny's distance data.

Two observations suggest that Ptolemy's southern coast of the Pontus was also affected by the westward shift of the Cimmerian Bosporus. First, as was noted above in footnote 22, the comparison of Ptolemy's data with Pseudo-Arrian reveals several abnormal coastal segments, which, although sufficiently long in Pseudo-Arrian, become even longer in Ptolemy. Two of these segments are located symmetrically on the opposite coasts of the Pontus and are almost equal in length, which can hardly be an accident: Kotyor–Trapezus on the southern coast is 1075 stades in Pseudo-Arrian and becomes 236 stades longer in Ptolemy, whereas Dioskurias–Toretika on the northern coast is 1070 stades in Pseudo-Arrian and becomes 253 stades longer in Ptolemy (Figs. 3, 6). Second, the lengthening of the Kotyor–Trapezus segment is counterbalanced by the shortening of Ptolemy's Sinope–Amisus segment by 272 stades subtracted from the 1030 stades that is recorded in Pseudo-Arrian. Remarkably, Ptolemy's Amisus is situated exactly on the meridian of Hermonassa (Fig. 1). It is tempting to suppose that there was a chain reaction of interconnected displacements, with the westward shift of the Cimmerian Bosporus including Hermonassa dragging Amisus to the west and causing the shortening of the Sinope–Amisus segment as well as symmetrically stretching the Kotyor–Trapezus segment.

10 Conclusions

The main conclusion of our study is that the configuration of the Pontus Euxinus described in Ptolemy's Geography can be explained as a result of using the same information that has come down to us through other ancient sources. Three types of data can be considered as the basic “constituent elements” of Ptolemy's map: the latitudes of the key points, the length of the coastlines, and the straight-line distances across the open sea. The method employed for revealing these elements is based on comparison with the other surviving sources, which yields the following results.

First, we have shown that Ptolemy's latitudes for many points on the coasts of the Pontus and Maeotis (Byzantium, Amisus, Trapezus, the mouth of the Borysthenes, the Cimmerian Bosporus, the mouth of the Tanais, and the mouth of the Phasis) are very close to those attested to by the earlier mathematical geographers (Eratosthenes, Hipparchus, and Marinus). In the same manner, a comparison of Ptolemy's data on the perimeter of the Pontus and the length of the coastal stretches between the key points (e.g. the Sanctuary of Artemis/Zeus Ourios, Cape Karambis, Sinope, Trapezus, the mouth of the Phasis, and so on) with the corresponding estimates reported by the other geographers (Eratosthenes, Artemidorus, Strabo, Arrian, and especially Pseudo-Arrian) reveals a close correlation between them. Furthermore, Ptolemy's configuration of the Pontus fits almost perfectly with the three straight-line distances across the open sea reported by Pliny the Elder (from the Thracian Bosporus to the Cimmerian Bosporus, from the latter to Cape Karambis, and from the mouth of the Maeotis to the mouth of the Tanais). As there is common consensus that the aforementioned correlations between latitude data imply that Ptolemy drew on earlier mathematical geographers, it is reasonable to conclude that similar correlations between distance data suggest that he drew on some sources of the Periplous type, especially those similar to Pseudo-Arrian's Periplous of the Pontus Euxinus.

Of course, there is no reason to think that Ptolemy used the same version of the Periplous that has come down to us. However, the nature of this kind of source – a compilation, aiming to combine all available information, and therefore open to further corrections and additions – suggests that there must have been a much larger number of similar versions of the Periplous of the Pontus circulating in antiquity than is directly attested to by the surviving sources. That is exactly the manner in which Pseudo-Arrian's Periplous was compiled from Menippus, Arrian and Pseudo-Scymnus; Pseudo-Scymnus, in turn, largely drew on his predecessors (Ephorus, Demetrius of Callatis, and others), and Arrian also extensively used written sources, possibly including Menippus (Diller, 1952; Podossinov, 2015). The fact that Pseudo-Arrian's distance data closely agree with those recorded by the earlier geographers (Eratosthenes, Artemidorus, Strabo, and Pliny) makes it likely that all of them ultimately drew on similar periploi (Tables 1, 2). It is reasonable to suppose that one of these periploi could be among Ptolemy's sources.

Possible explanations for the several conspicuous disagreements between Ptolemy's data and other sources have been suggested. Constant disagreements with Pseudo-Arrian's data on the distances between neighbouring coastal points can be explained by Ptolemy's tendency to smooth out the unevenness in the spatial distribution of the points along the coast: to lengthen short distances and to shorten the long distances. A drastic shortening of Ptolemy's west coast of the Pontus (between the Thracian Bosporus and the mouth of the Borysthenes) relative to the corresponding distances reported by the other sources is entirely explained by his underestimate of the circumference of the Earth. A symmetric lengthening of the north-eastern coastal stretch between the mouth of the Phasis and the Cimmerian Bosporus can be accounted for in part by Ptolemy's adoption of the straight-line distances across the open sea reported by Pliny. The adoption of these distances most likely caused a shift of the Cimmerian Bosporus to the west and a similar westward displacement of Amisus, which was located on the same meridian as Hermonassa on the Bosporus. These findings contribute to our better understanding of Ptolemy's logic for constructing his map of the Pontus.

In conclusion, the following explanation of Ptolemy's logic can be proposed as a working hypothesis. The construction of his map went through several stages proceeding from the most important and reliably located reference points to the less important and questionable, and from the most general outlines to increasingly smaller details. Four reference points can most naturally be selected as primary for constructing the outlines of the Pontus: the Thracian and Cimmerian Bospori, and the mouths of the Phasis and the Borysthenes. All of these points can be located using the existing latitude and distance data, which may be regarded as among the principal “constituent elements” of Ptolemy's map. The latitudes of the four references were established by the earlier mathematical geographers, and the coastal distances between them were reported by numerous periploi. However, the erroneous value of the circumference of the Earth accepted by Ptolemy created a contradiction between the latitudes of Byzantium (43^∘5^′) and the mouth of the Borysthenes (48^∘30^′) as well as the coastal distance between them, and Ptolemy chose to sacrifice the distance data as the less reliable. Another contradiction emerged between the positions of the Cimmerian Bosporus and the mouth of the Phasis. The former was determined by the latitude of the Borysthenes (48^∘30^′) and the straight-line distances from Cape Karambis and the Thracian Bosporus, whereas the latter was determined by the latitude of the middle of the Pontus (45^∘) and the coastline distance measured from the Thracian Bosporus, as well as by its reputation as the easternmost point of the Pontus. Combined, these elements imply that the Cimmerian Bosporus–Phasis coastal stretch must be much longer than was estimated by Pseudo-Arrian and other geographers. Therefore, this stretch, as the least explored section of the Black Sea coast, turned out to be the “weakest link” in the chain of information about the Pontus available to Ptolemy. It is unsurprising that he chose to sacrifice this link to fit other pieces of information together.

Appendix A

Corrections to the Ξ coordinates of the Pontus and Maeotis coastline (see Fig. 4).

1. Cape Akritas: its Ξ coordinates (43^∘35^′ lat., 56^∘15^′ long.) are an obvious mistake, because Ptolemy (5.1.2) places it on the coast of the Propontis (Sea of Marmara); the Ω values (42^∘45^′ lat., 56^∘30^′ long.) should be accepted.

2. Artake: its Ξ latitude μγ γιβ^′ (43^∘55^′) is an obvious mistake, because it creates a sharp northward bend that interrupts the integrity of the coastline; the Ω value (43^∘15^′) should be accepted.

3. Hypios: its Ξ coordinates (43^∘ lat., 58^∘50^′ long.) coincide with those of the next coastal point, the mouth of the Elata, and thus appears as a simple scribal error; the Ω values (42^∘45^′ lat., 56^∘30^′ long.) should be accepted.

4. Amastris: its Ξ longitude (62^∘30^′) displaces the city far from the coast, deep inside the continent, and is therefore an obvious mistake; the Ω value (60^∘30^′) should be accepted.

5. Hyssos Harbour: its Ξ longitude (70^∘45^′) coincides with that of the next coastal point, Trapezus, and causes the coastline to create an unnaturally acute angle; the Ω value (70^∘30^′) should be preferred, as it is more natural.

6. Rizus and Cape Adienon: the Ξ longitude of the latter (71^∘15^′) visually turns it from a cape to a gulf; therefore, the Ω value (71^∘) should be preferred as the more logical. If we accept the Ω longitude for Cape Adienon, the Ξ coordinates of Rizus can no longer be valid as they cause the coastline to cross itself; thus, the Ω values must also be preferred for Rizus.

7. Archabis, Xyline, Kissa, Apsorros, and the mouth of the Apsorros: the difference between the Ξ and Ω longitude values of these points is so slight that it is difficult to ascertain which variant was the original. However, there are three reasons why the Ω reading should be preferred. First, in the Ω version, all four points are clearly arranged in a straight line, whereas in Ξ, this line breaks apart. Second, the Ω longitude of the Archabis (71^∘55^′) should be preferred as a lectio difficilior, while the Ξ value (72^∘) can be explained as a rounding up of the former. Third, each of four points in the Ξ version take their longitude value from the Ω coordinates of the next point: Archabis from Xyline, Xyline from Kissa, and Kissa and Apsorros from the mouth of the Apsorros. After all, it is easier to explain the Ξ version as a corruption of the Ω than vice versa.

8. Apsorros: its Ξ longitude (72^∘40^′) contradicts the notion generally accepted in antiquity that the easternmost point of the Pontus is the mouth of the Phasis, whose Ptolemy's longitude is 72^∘30^′ in both recensions; in addition, the Ξ longitude of the Apsorros creates an unnatural zigzag in the coastline; hence, the Ω value (72^∘20^′) should be accepted as the more plausible alternative.

9. Chariustos: its Ξ latitude (45^∘30^′) puts it in the same position as the next coastal point, Aia, and thus appears to be a scribal error; therefore, the Ω value (45^∘15^′) should be accepted.

10. Thessyris: its Ξ latitude (47^∘20^′) causes the coastline be at an unnaturally acute angle; the Ω value (47^∘) can be tentatively preferred as the more natural.

11. Paniardis: its Ξ longitude (69^∘40^′) evidently breaks the integrity of the coastline; the Ω value (67^∘30^′) appears the more natural.

12. Cape Myrmekion: its Ω latitude (48^∘30^′) appears to be more logical, because Myrmekion is known to be situated 20 or 25 stades from the narrowest point of the Kerch Strait where Achilleion in Asia lies directly opposite the village of Porthmion (Pseudo-Arrian 77 [28B], 79 [50], 85 [56], 120 [91]) or to Parthenion (Strabo 7.4.5 C310; 11.2.6, 8 C494) in Europe. Achilleion (in both recensions) and Parthenion (only in Ω) are situated at a latitude of 48^∘30^′ which distinctly marks the southern limit of the Maeotis and the northern limit of the Pontus at the vicinity of Tamyrake and the mouth of the Borysthenes. If we consider the significance of this latitude as one of the seven κλíματα that constituted the most basic framework of Ptolemy's map, then the most natural solution is that Myrmekion should have been placed at this latitude too. However, the Ξ coordinates of Myrmekion (48^∘10^′ long.) and Parthenion (48^∘15^′ lat., 63^∘45^′ long.) cannot be explained away as a scribal corruption of the Ω values, and arguments of logic, symmetry or beauty are not sufficient to dismiss the manuscript reading.

13. Cape Philia: its Ξ longitude (58^∘30^′, νη^∘ L^′) can be explained as a simple scribal corruption of the Ω value (58^∘35^′, νη^∘ Lιβ^′) which can be tentatively preferred as lectio difficilior.